Інверсивний конгруентний метод
Ця стаття не має інтервікі-посилань. |
Інверсивний конгруентний метод (або генератор Ейхенауера - Лена, також можливо Ейченауера - Лехна) - метод генерації псевдовипадкових чисел, заснований на використанні зворотнього по модулю числа для генерації наступного члена послідовності.
Опис
ред.Інверсивний конгруентний метод був запропонований Ейченауером і Лехна в 1986 році[1] як заміна лінійному конгруентному методу, що не володіє гратчастою структурою.
Даний метод полягає в обчисленні послідовності випадкових чисел в кільці класів за модулем натурального числа .
Основною відмінністю від лінійного методу є використання при генерації послідовності числа зворотнього до попереднього елемента, замість самого попереднього елемента.
Параметрами генератора є[2]:
| — сіль | |
| — множник | |
| — приріст |
У випадку простого n
ред.Значення членів послідовності задається у вигляді:
if if
У випадку складеного n
ред.Якщо число є складеним, елементи послідовності обчислюються наступним чином:
Параметри підбираються таким чинном, щоб .
Період
ред.Послідовність періодична, причому період не перевищує розмірності кільця . Максимальний період досягається в разі, якщо многочлен є примітивним. Достатньою умовою максимального періоду послідовності є такий вибір констант і , щоб многочлен був незвідний[3].
У разі складеного максимально можливий період дорівнює (функція Ейлера)[4].
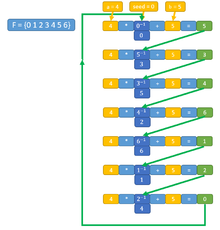
Приклад
ред.Інверсивний конгруентний генератор з параметрами генерує послідовність в кільці , де числа і , а також і протилежні один одному. В даному прикладі многочлен не можна звести в і числа не є його коренями, завдяки чому період максимальний і дорівнює .
Приклади реалізації
ред.Python
ред.def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
gcd, x, y = egcd(a, m)
if gcd != 1:
return None # modular inverse does not exist
else:
return x % m
def ICG(n, a, c, seed):
if (seed == 0):
return c;
return (a * modinv(seed, n) + c) % n;
seed = 1
n = 5
a = 2
c = 3
count = 10
for i in range(count):
print seed
seed = ICG(n, a, c, seed)
C++
ред.#include <iostream>
using namespace std;
int mod_inv(int a, int n)
{
int b0 = n, t, q;
int x0 = 0, x1 = 1;
if (n == 1) return 1;
while (a > 1)
{
q = a / n;
t = n, n = a % n, a = t;
t = x0, x0 = x1 - q * x0, x1 = t;
}
if (x1 < 0) x1 += b0;
return x1;
}
int ICG(int n, int a, int c, int seed)
{
if (seed == 0)
return c;
return (a * mod_inv(seed, n) + c) % n;
}
int main(void)
{
int seed = 1;
int n = 5;
int a = 2;
int c = 3;
int count = 10;
for (int i = 0; i < count; i++)
{
cout << seed << endl;
seed = ICG(n, a, c, seed);
}
return 0;
}
Складені інверсивні генератори
ред.Основним недоліком інверсивних конгруентних генераторів є зростання складності обчислень при збільшенні періоду. Даний недолік виправлений в складених інверсивних конгруентних генераторах.
Конструкція складених інверсивних генераторів є об'єднанням двох або більше інверсивних конгруентних генераторів.
Нехай - різні прості числа, кожне . Для кожного індексу в межах нехай - послідовність елементів з періодом . Іншими словами, .
Нехай - послідовність випадкових чисел в межах , де .
Результуюча послідовність визначається як сума: .
Період результуючої послідовності [5].
Одним з переваг даного підходу є можливість використовувати інверсивні конгруентні генератори працюючі паралельно.
Приклад складеного інверсивного генератора
ред.Нехай і . Для спрощення визначемо і . Для кожного обчислимо .
Тоді . Тобто ми отримаємо послідовність з періодом .
Щоб позбавитися від дробових чисел, помножимо кожен елемент отриманої послідовності на і отримаємо послідовність цілих чисел:
Переваги інверсивних конгруентних генераторів
ред.Інверсивні конгруентні генератори застосовуються в практичних цілях по ряду причин.
По-перше, інверсивні конгруентні генератори мають досить непогану рівномірність, крім того отримані послідовності абсолютно позбавлені гратчастої структури, характерної для лінійних конгруентних генераторів[6].
По-друге, числові послідовності, отримані за допомогою ІКГ не мають небажаних статистичних відхилень. Отримані даним методом послідовності перевірені рядом статистичних тестів і залишаються стабільними при зміні параметрів[7].
По-третє, складені генератори володіють тими ж властивостями, що і поодинокі лінійні інверсивні генератори, але при цьому мають період значно перевищуючий період одиночних генераторів. Крім того, пристрій складених генераторів дозволяє отримати високий приріст продуктивності при використанні на багатопроцесорних системах[8].
Існує алгоритм, що дозволяє розробляти складені генератори, що володіють довжиною періоду і рівнем складності, а також хорошими статистичними властивостями вихідних послідовностей[8].
Недоліки інверсивних конгруентних генераторів
ред.Основним недоліком інверсивних конгруентних генераторів є повільна швидкість генерації елементів послідовності: на обчислення одного елементу послідовності витрачається операцій множення.
Примітки
ред.- ↑ Кнут, 2013.
- ↑ Hellekalek, 1995, с. 255.
- ↑ Amy Glen: On the Period Length of Pseudorandom Number Sequences, 2002, с. 67, 5.3.
- ↑ Amy Glen: On the Period Length of Pseudorandom Number Sequences, 2002, с. 69, 5.4.
- ↑ Hellekalek, 1995, с. 256.
- ↑ Eichenauer-Herrmannn, Grothe, Niederreiter et al, 1990, с. 81.
- ↑ Hellekalek, 1995, с. 261.
- ↑ а б Bubicz, Stoklosa, 2006, с. 2.
