Алгоритм Тар'яна
Алгоритм Тар'яна — алгоритм пошуку компонент сильної зв'язності в орієнтованому графі, що працює за лінійний час.
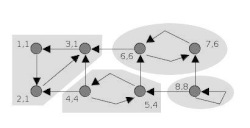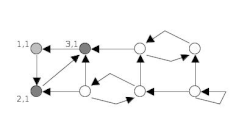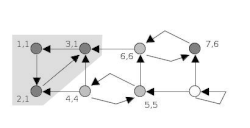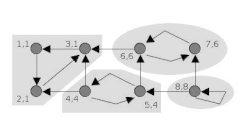 анімація алгоритму Тар'яна | |
| Структура даних | Граф |
|---|---|
| Найгірша швидкодія | |
Цей алгоритм ґрунтується на тому, що:
- Вершини розглядаються у зворотному топологічному порядку, тому в кінці рекурсивної функції для початкової вершини не зустрінеться жодна вершина з тієї ж сильної компоненти, оскільки всі вершини, досяжні з початкової, вже опрацьовано.
- Зворотні зв'язки в дереві дають інший шлях з однієї вершини в іншу і зв'язують сильні компоненти.
Неформальний опис алгоритму
ред.Алгоритм Тар'яна можна розуміти як варіацію алгоритму пошуку в глибину, в якому під час відвідування вершини і при закінченні опрацювання вершини виконуються додаткові дії. Відвідування вершини відбувається при русі від кореня до листя, а закінчення обробки вершини — на зворотному шляху. Під час відвідування вершини вона проштовхується в допоміжний стек, а виштовхується звідти при закінченні опрацювання[1].
Індекси компонент зв'язності всіх вершин зберігаються у векторі id, індексованому номерами вершин. Вектор low відстежує вершину з найменшим номером у прямому порядку обходу, досяжну з кожного вузла через послідовність прямих зв'язків, за якими слідує один висхідний зв'язок. Скориставшись пошуком у глибину з тим, щоб розглядати вершини в зворотному топологічному порядку, для кожної вершини v обчислюється максимальна точка, досяжна через зворотний зв'язок із попередника (low[v]). Коли для вершини v виконується pre[v]=low[v], вона виштовхується зі стека, а також всі вершини вище від неї і всім їм присвоюється номер компоненти[джерело?].
Час роботи
ред.Алгоритм має часову складність , де — кількість ребер, а — кількість вершин графу[1].
Простова складність становить , бо стек може вирости не більш ніж до (коли граф це одна велика компонента). Також ми зберігаємо додаткові ознаки для вершин.
Алгоритм у псевдокоді
ред.алгоритм Тар'яна це
вхід: граф G = (V, E)
вихід: множина компонент сильної зв'язності (множини вершин)
index := 0
S := порожній стек
для кожного v з V зробити
якщо v.index невизначений тоді
сильнозв'язна(v)
функція сильнозв'язна(v)
// Встановити індекс глибини для v у найменший незайнятий індекс
v.index := index
v.lowlink := index
index := index + 1
S.push(v)
v.onStack := істина
// Наступниці v
для кожного (v, w) з E зробити
якщо w.index невизначений тоді
// Цю наступницю w ше не відвідували; запускаємо рекурсію на ній
сильнозв'язна(w)
v.lowlink := min(v.lowlink, w.lowlink)
інакше, якщо w.onStack тоді
// Наступниця w на стеку S і, значить, в поточній КСЗ
// якщо w не на стеку, тоді (v, w) це ребро, що вказує на вже знайдену КСЗ і ми їм нехтуємо
// Примітка: Наступний рядок може виглядати дивним, але він правильний.
// Він використовує w.index, а не w.lowlink; це навмисно і було в оригінальній статті
v.lowlink := min(v.lowlink, w.index)
// Якщо v це корінь, то виштовхнути зі стеку і породити КСЗ
якщо v.lowlink = v.index тоді
розпочати нову компоненту сильної зв'язності
повторювати
w := S.pop()
w.onStack := хиба
додати w до поточної компоненти сильної зв'язності
допоки w ≠ v
вивести поточну компоненту сильної зв'язності
Змінна index це лічильник порядку вершини в обході в глибину. S це стек вершин, який напочатку порожній і зберігає історію досліджених вершин, які ще не були записані до якоїсь КСЗ. Зауважте, що це не звичаний стек пошуку в глибину, бо ми не виштовхуємо вершини з нього коли повертаємось вгору деревом, ми виштовхуємо їх лише коли повна компонента сильної зв'язності була знайдена.
Коли кожна вершина завершує рекурсію, якщо її lowlink все ще рівний її index, тоді це корінь компоненти сильної зв'язності, утвореної всіма вершинами вище в стеку. Алгоритм виштовхує зі стеку все вище цієї вершини і її саму записуючи всі ці вершини в нову компоненту.
Див. також
ред.- Алгоритм знаходження компонент сильної зв'язності — аналогічний алгоритм, що використовує пошук у глибину.
Примітки
ред.Література
ред.- Tarjan R. E. Depth-first search and linear graph algorithms // SIAM Journal on Computing. — 1972. — Vol. 1, no. 2 (14 January). — P. 146–160. — DOI:.
