Асимптотично паралельні прямі
У нейтральній або абсолютній геометрії і у гіперболічній геометрії може бути багато прямих, які паралельні даній прямій і таких, що проходять через точку за межами цієї прямої. Однак дві паралельні можуть бути ближчими до , ніж інші прямі (по одній з кожної сторони).
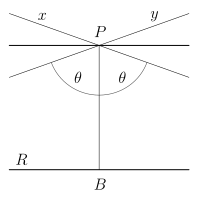
У цьому випадку можна дати інше визначення паралельності для нейтральної геометрії. Якщо є дуже близькі паралельні до даної прямої, їх називають асимптотично паралельними або паралельними до межі.
Для променів відношення асимптотичної паралельності є відношенням еквівалентності, яке включає термінальне відношення еквівалентності.
Асимптотичні паралельні можуть утворювати дві або три сторони асимптотичного трикутника.
Визначення
ред.Промінь є асимптотично паралельним променю , якщо вони котермінальні або якщо вони лежать на різних прямих, не рівних прямій , не перетинаються і будь-який промінь усередині кута перетинає промінь [1].
Властивості
ред.Різні прямі, що містять асимптотичні паралельні промені, що не перетинаються.
Доведення
ред.Припустимо, що прямі, які містять різні паралельні промені, перетинаються. За визначенням вони не можуть перетнутися на стороні , в якій знаходиться промінь . Тоді вони повинні перетинатися на стороні , яка є протилежною променю , позначивши цю точку . Тоді (тут P = прямий кут) . Суперечність.
Див. також
ред.Примітки
ред.- ↑ Hartshorne, Robin (2000). Geometry: Euclid and beyond (вид. Corr. 2nd print.). New York, NY [u.a.]: Springer. ISBN 978-0-387-98650-0.
Література
ред.- Robin Hartshorne. Geometry: Euclid and beyond. — New York, NY [u.a.] : Springer, 2000. — Т. Corr. 2nd print.. — ISBN 978-0-387-98650-0.

