Великий вивернутий оберненокирпатий ікосододекаедр
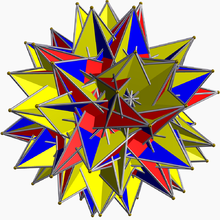
Вели́кий (ви́вернутий) оберненокирпа́тий ікосододекае́др — це неопуклий однорідний многогранник, що має індекс U74. Має 92 грані (80 трикутників і 12 п'ятикутників), 150 ребер і 60 вершин[1]. Його символ Шлефлі — s{3/2,5/3}.
| Великий вивернутий оберненокирпатий ікосододекаедр U74, K79, C90 | |
|---|---|
 | |
| Тип | однорідний зірчастий многогранник |
| Граней | 98 |
| Ребер | 150 |
| Вершин | 60 |
| χ | 2 |
| Символ Витофа | |3/2 5/3 2 |
| Символ Шлефлі | s{3/2,5/3} |
| Група симетрії | I, [5,3]+, 532 |
| Дуальний многогранник | великий пентаграмний шістдесятигранник[en] |
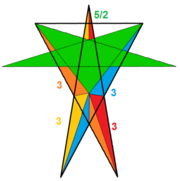
| Вершинна діаграма | |
 | |
Декартові координати
ред.Декартові координати вершин великого оберненокирпатого ікосододекаедра всі є парними перестановками: (±2α, ±2, ±2β),
- (±(α−βτ−1/τ), ±(α/τ+β−τ), ±(−ατ−β/τ−1)),
- (±(ατ−β/τ+1), ±(−α−βτ+1/τ), ±(−α/τ+β+τ)),
- (±(ατ−β/τ−1), ±(α+βτ+1/τ), ±(−α/τ+β−τ)) і
- (±(α−βτ+1/τ), ±(−α/τ−β−τ), ±(−ατ−β/τ+1)), з парним числом знаків «+», де
- α = ξ−1/ξ
і
- β = −ξ/τ+1/τ2−1/(ξτ), де τ = (1+ √5)/2 — золотий перетин, а ξ — найменший додатний дійсний нуль функції ξ3−2ξ=−1/τ, а саме
що приблизно дорівнює 0,3264046. Якщо взяти непарні перестановки координат вище з непарним числом знаків плюс, отримаємо іншу, енантіоморфну, форму. Якщо взяти непарні перестановки з парним числом знаків плюс чи навпаки, отримаємо ті ж тіла, повернуті на 90°.
Радіус описаної сфери для тіла з одиничним ребром дорівнює
- ,
де — відповідний нуль функції . Чотири додатні дійсні корені рівняння шостого степеня в
є радіусами описаних сфер кирпатого додекаедра (U29), великого кирпатого ікосододекаедра[en] (U57), великого вивернутого кирпатого ікосододекаедра[en] (U69) і великого оберненокирпатого ікосододекаедра (U74).
Див. також
ред.Примітки
ред.- ↑ Maeder, Roman. 74: great retrosnub icosidodecahedron. MathConsult.
{{cite web}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання)
Посилання
ред.- Weisstein, Eric W. Великий вивернутий оберненокирпатий ікосододекаедр(англ.) на сайті Wolfram MathWorld.
- https://web.archive.org/web/20171110075259/http://gratrix.net/polyhedra/uniform/summary/