Розмірність простору
кількість координат простору для визначення положення
(Перенаправлено з Вимір (математика))
Розмі́рність, вимір, вимірність (англ. dimension) — кількість незалежних параметрів (вимірів), необхідних для опису стану об'єкта, або кількості ступенів вільності фізичної або абстрактної системи.
| Розмірність простору | |
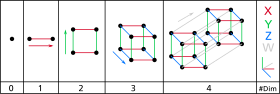 | |
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
|---|---|
| Є кількістю | напрямок |
| | |
Поняття виміру не обмежується лише фізичними об'єктами. Багатовимірні простори часто зустрічаються в математиці та інших науках. Це можуть бути параметричні[en] чи конфігураційні простори механіки Лагранжа чи Гамільтона; це абстрактні простори, не пов'язані з фізичним простором в якому ми живемо.
Визначення
ред.У математиці існує кілька різних підходів до визначення розмірності, наприклад
- Розмірність векторного простору
- Комбінаторна розмірність множини визначається на підставі її комбінаторних властивостей і може бути довільним невід'ємним числом[1].
- Загальніші визначення дано в теорії розмірності
- Розмірність Лебега, або топологічна розмірність.
- Розмірність Гаусдорфа метричного простору.
- Розмірність Мінковського допускає узагальнення на фрактали, при цьому їх розмірність може бути довільним невід'ємним числом.
Приклади
ред.- Для того, щоб описати стан кола на площині, достатньо трьох параметрів: двох координат центру і радіусу, тобто: простір кіл на площині — тривимірний; простір точок на тій же поверхні — двовимірний; тим не менше саме коло-простір точок на колі- одновимірний: будь-яка його точка може бути описана одним параметром.
- У рамках ходових моделей поверхні нашої планети для визначення положення міста (місто при цьому розглядається не як двовимірний об'єкт, а як точка) на поверхні Землі достатньо двох параметрів, а саме: географічної широти та географічної довготи. Відповідно: простір у таких моделях є двовимірним (скорочено — 2D, від англ. dimension), див. геопростір.
- У рамках ходових моделей нашої фізичної реальності для визначення положення деякого об'єкта, наприклад — літака (літак при цьому розглядається не як тривимірний об'єкт, а — як точка), потрібно вказати три координати — додатково до широти і довготи потрібно знати висоту, на якій він знаходиться. Відповідно: простір у таких моделях є тривимірним (3D). До цих трьох координатах може бути додана четверта (час) для опису не тільки поточного положення літака, але і моменту часу. Якщо додати в модель орієнтацію (крен, тангаж, рискання) літака, то додадуться ще три координати і відповідний абстрактний простір моделі стане семивимірним.
Див. також
ред.Примітки
ред.- ↑ R. BleiAnalysis in integer and fractional dimensions, — New-York: Cambridge university press, — 556 p. — 2003. — ISBN 0-511-01266-7 (netLibrary Edition), ISBN 0-521-65084-4 (hardback).
Література
ред.- Murty, Katta G. (2014). 1. Systems of Simultaneous Linear Equations (PDF). Computational and Algorithmic Linear Algebra and n-Dimensional Geometry. World Scientific Publishing. doi:10.1142/8261. ISBN 978-981-4366-62-5.
- Abbott, Edwin A. (1884). Flatland: A Romance of Many Dimensions. London: Seely & Co.
- —. Flatland: ... Project Gutenberg.
- —; Stewart, Ian (2008). The Annotated Flatland: A Romance of Many Dimensions. Basic Books. ISBN 978-0-7867-2183-2.
В іншому мовному розділі є повніша стаття Dimension(англ.). Ви можете допомогти, розширивши поточну статтю за допомогою перекладу з англійської.
|
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |