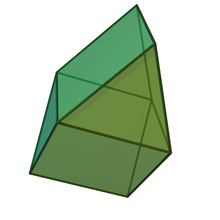
Гіробіфастигіум

Гіробіфастигіум або двосхилий повернутий бікупол є 26-м многогранником Джонсона (J₂₆). Його можна побудувати, об'єднавши дві трикутні призм з правильними гранями відповідними квадратним гранями з поворотом однієї призми на 90º. Це єдине тіло Джонсона, яким можна заповнити тривимірний простір.

Гіробіфастигіум

Історія та назва

Многогранник Джонсона є одним з 92 строго опуклих многогранників, що мають правильні грані, але не є однорідними многогранниками (тобто не є платоновими тілами, архімедовими тілами, призмами або антипризмами). Тіла названо ім'ям Нормана Джонсона, який вперше перелічив їх 1966 року.

Назва гіробіфастигіум походить від латинського слова fastigium, що означає двосхилий дах. У стандартних домовленостях про найменування тіл Джонсона бі- означає з'єднання двох тіл за їх основами, а гіро- означає дві половинки, повернуті одна відносно одної.

Положення гіробіфастигіума в списку тіл Джонсона безпосередньо перед бікуполом пояснюється тим, що його можна розглядати як двокутний гіробікупол. Подібно до того, як інші правильні куполи мають чергування квадратів і трикутників, що оточують багатокутник у вершині (трикутник , квадрат або пятикутник), кожна половина гіробіфастигіума складається з почергових квадратів і трикутників, з'єднаних угорі ребром.

Стільники

Повернутий трикутний призматичний стільник можна побудувати, упаковуючи багато однакових гіробіфастигіумів. Гіробіфастигіум є одним з п'яти опуклих многогранників з правильними гранями, здатних заповнити простір (інші чотири — куб, зрізаний октаедр, трикутна і шестикутна призми), і єдине тіло Джонсона з цією властивістю.

Біпризма Шмітта-Конвея-Данцер

Формули

Наведені далі формули для об'єму і площі поверхні можна використовувати, якщо всі грані є правильними багатокутниками з ребрами довжини a:

$V=({\frac {\sqrt {3}}{2}})a^{3}\approx 0.866025...a^{3}$

$A=(4+{\sqrt {3}})a^{2}\approx 5.73205...a^{2}$

Топологічно еквівалентні многогранники

Біпризма Шмітта — Конвея — Данцера

Біпризма Шмітта — Конвея — Данцера (або протоплитка SCD) є многогранником, топологічно еквівалентним гіробіфастигіуму, але з гранями у формі паралелограма і неправильних трикутників замість квадратів і правильних трикутників. Подібно до гіробіфастигіума, цей многогранник може заповнити простір, але тільки аперіодично або з гвинтовою симетрією , а не з повною групою тривимірної симетрії. Таким чином, цей многогранник дає частковий розв'язок тривимірної задачі однієї плитки.

Двоїстий многогранник гіробіфастигіума

Біфастигіум

Пов'язані многогранники

Двоїстий многогранник гіробіфастигіума має 8 граней — 4 рівнобедрених трикутники, відповідних вершинам степеня 3, і 4 паралелограми, відповідних вершинам степеня 4.

Біфастигіум (дігональний ортобікупол), подібно до гіробіфастигіума, утворений склеюванням двох рівносторонніх трикутних призм бічними квадратними гранями, але без повороту. Він не є тілом Джонсона, оскільки його трикутні грані копланарні (лежать в одній площині). Однак існує самодвоїстий опуклий многогранник з неправильними гранями, що має таку ж комбінаторну структуру. Цей многогранник схожий з гіробіфастигіумом у тому, що вони мають по вісім вершин і вісім граней, з гранями, що утворюють пояс із чотирьох квадратних граней, які розділяють дві пари трикутників. Однак у двоїстому гіробіфастигіумі дві пари трикутників повернуті одна відносно іншої, а в біфастигіумі не повернуті.

Література

• S. M. Nazrul Alam, Zygmunt J. Haas. Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom '06). — New York, NY, USA : ACM, 2006. — P. 346–357. — ISBN 1-59593-286-0. — DOI:10.1145/1161089.1161128.
• Johannes Kepler. [1] — Paul Dry Books, 2010. — ISBN 9781589882850. Архівовано з джерела 11 квітня 2016 Виноска 18
• David J. Darling. [2] — John Wiley & Sons, 2004. — ISBN 9780471667001. Архівовано з джерела 15 квітня 2016
• Norman W. Johnson. Convex polyhedra with regular faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — DOI:10.4153/cjm-1966-021-8.
• Anthony Rich. Dictionary of Greek and Roman Antiquities / William Smith. — London : John Murray, 1875.
• Marjorie Senechal. [3] — Cambridge University Press, 1996. — ISBN 9780521575416. Архівовано з джерела 19 серпня 2020
• В. А. Залгаллер. Выпуклые многогранники с правильными гранями // Зап. научн. сем. ЛОМИ. — 1967. — Т. 2.

Посилання

• Weisstein, Eric W. Гіробіфастигіум(англ.) на сайті Wolfram MathWorld.