Джойн (топологія)
В топології джойн (іноді з'єднання) двох топологічних просторів A і B визначається як фактор-простір
де I — це відрізок [0, 1], а відношення еквівалентності має такий вигляд:
а при точка еквівалентна сама собі. Таким чином, джойн стискає у , а — у .
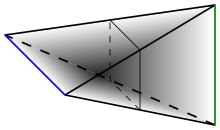
З інтуїтивної точки зору, джойн утворюється шляхом незв'язного об'єднання двох просторів та проведенням усіх можливих відрізків, що з'єднують кожну точку з A з усіма точками з B.
Приклади
ред.- Джойн простору і простору, що складається з однієї точки, має назву конуса простора .
- Джойн простору і нуль-вимірної сфери (тобто, дискретного простору з двох точок) має назву надбудови простора .
- Джойн двох сфер і — це сфера .
- Джойн n точок — це опуклий (n-1)-вимірний багатогранник, що має назву (n-1)-симплекса.
Література
ред.- Васильев В. А. Введение в топологию. — М. : Фазис, 1997. — 132 с.
- Хатчер А. Алгебраическая топология = Algebraic Topology. — М. : МЦНМО, 2011. — 688 с.
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |









