Логічна еквівалентність
Логічна еквівалентність (еквіваленція) — двомісна логічна операція, що має значення «істина» тоді і тільки тоді, коли обидва операнди мають однакове значення. В інших випадках еквіваленція буде хибною. Операція відображає вживання сполучника «тоді і тільки тоді» в логічних висловлюваннях.
| EQ, XNOR | |
|---|---|
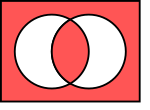 | |
| Визначення | |
| Таблиця істинності | |
| Логічний вентиль | |
| Нормальні форми | |
| Диз'юнктивна | |
| Кон'юнктивна | |
| Алгебрична | |
| Ґратка Поста | |
| (зберігає 0) | ✗ |
| (зберігає 1) | |
| (монотонна) | ✗ |
| (лінійна) | |
| (само-двоїста) | ✗ |
Еквівалентність позначають символами: , .
( , ).
Висловлення є правдивим тоді і тільки тоді, коли водночас правдиві обидві імплікації та , тобто:
- .
У природній мові аналогами еквіваленції є вирази:
- A тоді і тільки тоді, коли B
- A якщо B і B якщо A
- Для A достатньо і необхідно B
- A матеріально еквівалентно B
Визначення
ред.Таблиця істинності виглядає таким чином:
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | T |
Ця таблиця відрізняється від таблиці істинності для імплікації другим рядком, а від таблиці істинності для конверсії імплікації — третім рядком.
Також еквівалентність є запереченням виключної диз’юнкції, тобто
| F | F | T | F |
| F | T | F | T |
| T | F | F | T |
| T | T | T | F |
Оскільки імплікація виражає відношення між достатньою умовою та її наслідком, а конверсія імплікації — між необхідною умовою та її наслідком, то еквіваленція або подвійна імплікація, виражає відношення між достатньою і необхідною умовою та її наслідком.
Наприклад, "Якщо він знає англійську мову, то він перекладе цей текст", "Якщо геометрична фігура квадрат, то її діагоналі діляться навпіл". Як у матеріальній імплікації сполучник "якщо, то ..." не виражає смислового зв'язку між антецедентом і консеквентом, так і в еквіваленції сполучник "якщо і тільки якщо" не виражає змістовно зв'язку між лівою і правою частинами еквівалентності; він виражає лише відношення між їх істинними значеннями ("істина", "хибність"). Ця особливість еквіваленції відіграє важливу роль для операцій із символами у логічних численнях.
Знання логічної еквіваленції дає можливість:
- а) спростити запис послідовності висловлювань;
- б) перейти від одного висловлювання до логічно еквівалентного йому (тобто, з тим самим істинним значенням);
- в) замінити у послідовності формул одні формули на інші.
Властивості
ред.Функціональна повнота
ред.Множина операцій є функціонально повною:
...
Дивись також
ред.Джерела і посилання
ред.- Конверський А. Є. Логіка: Підручник для студентів юридичних факультетів. — К.: Центр навчальної літератури, 2004. — 304 с. ISBN 966-8568-48-6
Література
ред.- Еквівалентність // Філософський енциклопедичний словник / В. І. Шинкарук (гол. редкол.) та ін. — Київ : Інститут філософії імені Григорія Сковороди НАН України : Абрис, 2002. — 742 с. — 1000 екз. — ББК 87я2. — ISBN 966-531-128-X.
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |
















