Кеплерові елементи орбіти
Кеплерові елементи — шість елементів орбіти, що визначають положення небесного тіла в просторі у задачі двох тіл:
- велика піввісь (),
- ексцентриситет (),
- нахил (),
- довгота висхідного вузла (),
- аргумент перицентру (),
- середня аномалія ().
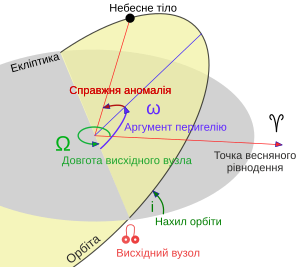

Перші два визначають форму орбіти, третій, четвертий і п'ятий - орієнтацію площини орбіти по відношенню до базової системи координат, шостий - положення тіла на орбіті.
Велика піввісь
ред.Велика піввісь — це половина головної осі еліпса (позначена на рис.2 як a). В астрономії характеризує максимальну відстань небесного тіла від центру еліптичної орбіти.
Ексцентриситет
ред.Ексцентрисите́т (позначаеться « » чи «ε») — числова характеристика конічного перетину. Ексцентриситет інваріантний щодо рухів площини і перетворень подібності.[1] Ексцентриситет характеризує «стислість» орбіти. Він виражається за формулою:
- , де — мала піввісь (див. рис.2)
Можна розділити зовнішній вигляд орбіти на п'ять груп:
Нахил
ред.B — Центральний об'єкт
C — Площина відрахунку
D — Площина орбіти
i — Нахил
Нахил орбіти небесного тіла — це кут між площиною його орбіти і площиною відліку (базовою площиною).
Зазвичай позначається буквою i (від англ. Inclination). Нахил вимірюється в кутових градусах мінутах і секундах.
- Якщо °, то рух небесного тіла називається прямим.
- Якщо ° °, то рух небесного тіла називається зворотним.
У застосуванні до Сонячної системи, за площину відліку зазвичай вибирають площину орбіти Землі (площину екліптики). Площини орбіт інших планет Сонячної системи і Місяця відхиляються від площини екліптики лише на кілька градусів.
Довгота висхідного вузла
ред.Довгота висхідного вузла - один з основних елементів орбіти, що використовується для математичного опису орієнтації площини орбіти відносно базової площини. Визначає кут в базовій площині, утворений між базовим напрямком на нульову точку і напрямком на точку висхідного вузла орбіти, в якій орбіта перетинає базову площину в напрямку з півдня на північ.
Аргумент перицентру
ред.Аргуме́нт перице́нтру — визначається як кут між напрямками з притягувального центру на висхідний вузол орбіти і на перицентр (найближчу до притягувального центру точку орбіти супутника), або кут між лінією вузлів і лінією апсид. Відраховується з притягувального центру в напрямку руху супутника звичайно вибирається в межах 0°-360°.
При дослідженні екзопланет і подвійних зірок як базову використовують картинну площину - площину, що проходить через зірку і перпендикулярну променю спостереження зірки з Землі. Орбіта екзопланети в загальному випадку випадковим чином орієнтована щодо спостерігача, перетинає цю площину в двох точках. Точка, де планета перетинає картинну площину, наближаючись до спостерігача, вважається висхідним вузлом орбіти, а точка, де планета перетинає картинну площину, віддаляючись від спостерігача, вважається низхідним вузлом. У цьому випадку аргумент перицентру відраховується з притягувального центру проти годинникової стрілки.
Позначається ( ).
Замість аргументу перигелію часто використовується інший кут довгота перигелію що позначається як . Він визначається, як сума довготи висхідного вузла і аргументу перигелію. Це - дещо незвичний кут, так як він вимірюється частково вздовж екліптики, а частково - уздовж орбітальної площини. Однак, часто він більш практичний, ніж аргумент перигелію, так як добре визначений навіть, коли нахил орбіти близько до нуля, коли напрямок на висхідний вузол стає невизначеним[2].
Середня аномалія
ред.Середня аномалія для тіла, що рухається по незбуреній орбіті - добуток його середнього руху та інтервалу часу після проходження перицентру. Таким чином, середня аномалія - кутова відстань від перицентру гіпотетичного тіла, що рухається з постійною кутовою швидкістю, що дорівнює середньому руху.
Позначається буквою (від англ. mean anomaly)
У зоряної динаміці середня аномалія M обчислюється за такими формулами:
де:
- — середня аномалія на епоху ,
- — початкова епоха,
- — епоха, на яку здійснюються обчислення, і
- — середній рух.
Або через рівняння Кеплера:
де:
- — ексцентрична аномалія ( на рис.3),
- — ексцентриситет.
Обчислення кеплерових елементів
ред.Розглянемо наступну задачу: нехай є необуреним рух і відомі вектор положення і вектор швидкості на момент часу . Знайдемо кеплерові елементи орбіти.
Перш за все, обчислимо велику піввісь:
За інтегралом енергії:
- (1) , де μ — гравітаційний параметр, що дорівнює добутку гравітаційної постійної на масу небесного тіла; для Землі μ = 3,986005·105 км³/c², для Сонця μ = 1,32712438·1011 км³/c².
Таким чином, по формулі (1) знаходимо .
Див. також
ред.Примітки
ред.- ↑ А. В. Акопян, А. А. Заславский Геометрические свойства кривых второго порядка, [Архівовано 20 березня 2018 у Wayback Machine.] — М.: МЦНМО, 2007. — 136 с.
- ↑ Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner. 6.





