Книжкове вкладення
Книжкове вкладення в теорії графів — узагальнення планарного вкладення графа до вкладення в книжку — набір напівплощин, які мають межею одну й ту саму пряму. Зазвичай потрібно, щоб вершини графа лежали на цій межі, а ребра мають міститися всередині однієї сторінки. Книжкова товщина (або кількість сторінок) графа — найменша кількість напівплощин серед усіх книжкових вкладень графа.[1] Книжкове вкладення використовують для деяких інших інваріантів графа, серед яких ширина сторінки[2] та книжкове число схрещень[3].
Будь-який граф з вершинами має книжкову товщину не більше . Ця межа близька до повних графів[1]. Однак поділ кожного ребра може зменшти книжкову товщину до величини, пропорційної кореню квадратному з .[4] Графи з книжковою товщиною один є зовніпланарними графами,[1] а графи з книжковою товщиною не більше двох є підгамільтоновими, які завжди планарні[2]. Будь-який планарний граф має книжкову товщину, що не перевищує чотирьох[5]. Всі мінорно замкнуті сімейства графів, і, зокрема, графи з обмеженою деревною шириною або обмеженим родом, також мають обмежену книжкову товщину[6]. Визначення точної книжкової товщини заданого графа є NP-складною задачею, незалежно від того, чи відомий порядок вершин на корінці[7][8].
Одним із початкових приводів вивчення книжкового вкладення було його застосування в розробці НВІС, де вершини книжкового вкладення представляють компоненти, а ребра — з'єднання між ними[7][9]. При візуалізації графів за допомогою книжкового вкладення можна побудувати два стандартні стилі подання графів: дугові діаграми[10] та колові розташування [11],. Різні початкові та кінцеві точки руху пішоходів і машин, що регульованого світлофором, можна математично змоделювати як вершини графа, а ребра будуть представляти пари початок-кінець, книжкове ж вкладення цього графа можна використати для розробки режиму роботи світлофора, щоб забезпечити регулювання руху з найменшим числом станів світлофора[12]. У задачах біоінформатики, що працюють зі структурами РНК, односторінкове книжкове вкладення представляє класичну форму вторинної структури нуклеїнової кислоти[en], а двосторінкове вкладення представляє псевдовузли[13]. Книжкове вкладення використовують також у загальній алгебрі [14] та теорії вузлів[15][16].
Відкритими проблемами, що стосуються книжкового вкладення, є
- Чи обмежена книжкова товщина довільного графа функцією його підрозбиттів?[17]
- Чи достатньо знати порядок вершин на корінці, щоб перевірити, чи граф має тристорінкове вкладення?[18]
- Чи існує планарний граф, книжкова товщина якого дорівнює чотирьом?[19]
- Скільки перетинів на корінці необхідно для тристорінкового топологічного вкладення (у цьому випадку ребра можуть переходити зі сторінки на сторінку через корінець) довільного графа?[20]
Історія
ред.Назву «книга» ввели Персінгер і Атнеосен (C. A. Persinger, Gail Atneosen) у 1960-ті роки[21][22][23]. Атнеосен вже використовував вкладення графів у книги, але формально концепцію книжкового вкладення сформулювали Кайнен та Оллман (C. Kainen, L. Taylor Ollman) на початку 1970-х і додали деякі обмеження на спосіб вкладення — в їхньому формулюванні вершини графа мають лежати на корінці книги, кожне ребро має лежати на одній сторінці (не перетинати корінець) і будь-які два ребра перетинаються тільки в спільних кінцевих вершинах[24][25].
Важливими віхами в подальшому розвитку книжкового вкладення є доведення Міхаліса Яннакакіса наприкінці 1980-х, що книжкова товщина планарних графів не перевищує чотирьох[26][5], і відкриття наприкінці 1990-х тісного зв'язку між книжковим вкладенням та біоінформатикою[13].
Визначення
ред.Книга є частковим випадком топологічного простору (називана також віялом півплощин)[21][27]. Він складається з однієї прямої ℓ, званої корінцем[28] книги, разом з набором з однієї або більше півплощин, званих сторінками або аркушами книги. Кожна півплощина повинна мати межею ту саму пряму ℓ. Книги зі скінченним числом ( ) сторінок можна вкласти в тривимірний простір, наприклад, за допомогою вибору як прямої ℓ осі прямокутної системи координат, а як -ту сторінку (з ) можна взяти множину точок , таких що найкоротший відрізок, що з'єднує з віссю утворює з площиною кут [1].
Візуалізація книги скінченного графа у книгу — це малюнок графа у , такий що будь-яка вершина графа малюється на корінці , а будь-яке ребро малюється як крива, що лежить усередині однієї сторінки . -сторінкове книжкове число перетинів графа — це найменше число перетинів у малюнку на -сторінковій книзі[3].
Книжкове вкладення графа у — це вкладення графа у простір . Тобто це малюнок графа в , при якому ребра не перетинаються. Будь-який скінченний граф має книжкове вкладення в книгу з достатнім числом сторінок. Наприклад, завжди є можливість вкласти кожне ребро на свою сторінку. Товщина книги, число сторінок, або стекове число графа — це найменша кількість сторінок, потрібна для книжкового вкладення графа . Інший параметр, який вимірює якість книжкового вкладення, крім кількості сторінок, — це ширина сторінки — найбільше число ребер всередині окремої сторінки, які перетинає промінь, перпендикулярний до корінця. Еквівалентно (для книжкових вкладень, у яких кожне ребро намальоване як монотонна крива), це найбільший розмір підмножини ребер, таких що інтервали, визначені на корінці кінцевими точками ребер, всі перетинаються[2][29][30].
Істотно для цих визначень, що ребра можуть лежати лише на одній сторінці. Як зазначив Амеозен, якщо ребра можуть переходити зі сторінки на сторінку (через корінець), то будь-який граф можна вкласти в тристорінкову книгу[22][31][20]. Однак для тристорінкового топологічного книжкового вкладення, в якому перетин корінця дозволено, залишається цікавою задача визначення найменшої кількості перетинів корінця, що дозволяє вкласти граф у книгу[20][32].
Конкретні графи
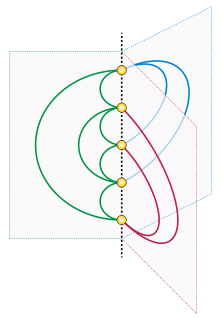
ред.Як показано на першому малюнку, книжкова товщина повного графа дорівнює трьом. Оскільки він не планарний, його книжкова товщина більше двох, але існує книжкове вкладення з трьома сторінками. Книжкова товщина будь-якого повного графа з вершинами дорівнює рівно . Цей результат дає верхню межу найбільшої книжкової товщини будь-яких графів вершинами[1]. Двосторінкова кількість перетинів повного графа дорівнює
що відповідає недоведеній гіпотезі Ентоні Гілла[en]. Тобто, якщо гіпотеза Гілла істинна, то малюнком цього графа, що мінімізує число перетинів, є двосторінковий малюнок[33].
Товщина книги повного двочасткового графа майже дорівнює — для кожної вершини меншої частки можна розташувати ребра, інцидентні цим вершинам, на власній сторінці. Ця межа не завжди строга. Наприклад, має товщину книги три, а не чотири. Однак, коли дві сторони графа дуже розбалансовані, , товщина книги дорівнює рівно .[1][34] Товщина книг двійкових графів де Брейна, графів тасованого обміну, і кубічних сіток із циклами[en] (коли ці графи досить великі, щоб не бути планарними) дорівнює рівно трьом[35].
Властивості
ред.Поведінка під час підрозбиттів
ред.| Нерозв'язана проблема математики: Чи може книжкова товщина графа бути обмежена функцією книжкової товщини підрозбиттів? (більше нерозв'язаних проблем математики)
|
Розбиття кожного ребра графа на двореберні шляхи додаванням нових вершин для кожного ребра може іноді збільшити книжкову товщину (наприклад, алмаз має книжкову товщину один, але його підрозбиття має книжкову товщину два). Однак таке підрозбиття може істотно зменшити книжкову товщину графа після розбиття. Наприклад, книжкова товщина повного графа пропорційна числу його вершин, але розбиття кожного ребра на два дає підрозбиття зі значно меншою книжковою товщиною, лише [4]. Попри існування прикладів, подібних до наведеного вище, Бланкеншип і Опоровські[31] висловили гіпотезу, що книжкова товщина підрозбиттів не може бути істотно меншою, ніж у початкового графа. Зокрема, вони припустили, що існує певна функція , що для будь-якого графа і графа , отриманого заміною кожного ребра шляхом із двох ребер, якщо книжкова товщина графа дорівнює , то книжкова товщина графа не перевищує .[31] До 2013 року гіпотеза Бланкеншипа — Опоровські залишалася недоведеною[17].
Планарність та зовнішня планарність
ред.Книжкова товщина даного графа не перевищує 1 тоді й лише тоді, коли зовніпланарний. Зовніпланарний граф — це граф, що має планарне вкладення, в якому всі вершини належать до зовнішньої грані вкладення. Для таких графів розташування вершин уздовж корінця в тому ж порядку, в якому вони з'являються на зовнішній грані (за повторної появи вершини на зовнішній грані береться лише одна копія вершини) дає односторінкове вкладення графа. І навпаки, односторінкове книжкове вкладення є автоматично зовніпланарним — якщо граф вкладено в одну сторінку, приєднання другої півплощини дає повну площину, а зовнішня грань міститиме всю додану півплощину, при цьому всі вершини лежатимуть на цій зовнішній грані[1][2].
Будь-яке книжкове вкладення з двома сторінками є окремим випадком планарного вкладення, оскільки об'єднання двох сторінок є простором, топологічно еквівалентним площині. Таким чином, будь-який граф із книжковою товщиною два автоматично є планарним. Точніше, книжкова товщина графа не більше двох тоді й лише тоді, коли є підграфом планарного графа, який має гамільтонів цикл[1]. Якщо дано граф із книжковим вкладенням у дві сторінки, граф можна розширити до планарного гамільтонового графа, додавши (на будь-якій сторінці) ребера між будь-якими двома послідовними вершинами вздовж корінця, якщо вони ще не з'єднані ребром, а також між першою та останньою вершиною корінця. Граф Голднера — Харарі є прикладом планарного графа, який має книжкову товщину два — це максимальний планарний граф, отже, неможливо додати жодного ребра, зберігаючи планарність, і граф не має гамільтонового циклу[1]. Зважаючи на вимогу наявності гамільтонових циклів, графи, що дозволяють двосторінкове вкладення, відомі як підгамільтонові графи[2].
Всі планарні графи з найбільшим степенем, що не перевищує чотирьох, мають товщину книжкового вкладення, що не перевищує двох[36]. Планарні 3-дерева мають найбільшу товщину книги, рівну трьом[37]. Усі планарні графи мають книжкову товщину, що не перевищує чотирьох[26][5]. Як стверджував Міхаліс Яннакакіс 1986 року[26], існують планарні графи з товщиною книжкового вкладення, точно рівною чотирьом, проте детальне доведення цього твердження, анонсоване в статті[5], так і не було опубліковане. Тому Дуймович[19] позначив задачу визначення найбільшої товщини книжкового вкладення планарних графів як нерозв'язану[19].
Зв'язок із іншими інваріантами графів
ред.Книжкова товщина пов'язана з товщиною графа, числом планарних графів, необхідних для покриття ребер заданого графа. Граф має товщину θ, якщо його можна вкласти в площину, і при цьому ребра можна розфарбувати в θ кольорів так, що ребра одного кольору не перетинаються. Аналогічно граф має книжкову товщину θ, якщо його можна намалювати в півплощині з вершинами на межі півплощини та розфарбувати ребра в θ кольорів без перетинів ребер одного кольору. За такого формулювання ребра одного кольору відповідають сторінкам книжкового вкладення. Однак товщина графа і книжкова товщина можуть істотно відрізнятися — існують підрозділи повних графів, що мають необмежену книжкову товщину[31][20][4], попри те, що товщина графа дорівнює двом[4].
Графи з деревною шириною мають книжкову товщину, яка не перевищує [19][38] і ця межа досягається для [19]. Графи з ребрами мають книжкову товщину [39], а графи з родом — книжкову товщину [40]. Загальніше, будь-яке мінорно-замкнуте сімейство графів має обмежену книжкову товщину[6][41].
Будь-який стягувальний мінор графа обмеженої книжкової товщини є розрідженим графом, у якого відношення числа ребер до числа вершин обмежене сталою, яка залежить лише від глибини мінору та книжкової товщини. Тобто, в термінології Нешетрила[6], графи з обмеженою книжковою товщиною мають обмежений зріст[6]. Однак навіть графи з обмеженим степенем графа (істотно сильніша вимога обмеження зросту) можуть мати необмежену книжкову товщину[42].
Оскільки графи з книжковою товщиною два є планарними графами, вони задовольняють теоремі про планарне розбиття — вони мають сепаратори, підмножини вершин, видалення яких ділить граф на частини з максимум вершинами в кожній частині, тільки з вершинами в сепараторі, де — кількість вершин графа. Однак існують графи з книжковою товщиною три, що не мають сепараторів сублінійного розміру[43].
Ребра на одній сторінці книжкового вкладення поводяться подібно до стеку. Це можна формалізувати, якщо розглянути довільну послідовність операцій push і pop (засилання та видобування) на стеку і сформувати граф, у якому стекові операції відповідають вершинам графа, розташованим на корінці книжкового вкладення в порядку виконання операцій. Якщо тепер намалювати ребро від кожної операції pop, що видобуває об'єкт зі стека, до операції push, яка заслала цей елемент у стек, отриманий граф автоматично матиме односторінкове вкладення. З цієї причини кількість сторінок графа називають також його стековим числом. Аналогічно дослідники визначають чергове вкладення графа як малюнок графа в книзі, в якому будь-які два ребра на сторінці або перетинаються, або покривають на корінці інтервали, що не перетинаються. Такі вкладення відповідають певним чином чергам і найменша кількість сторінок, необхідних для чергового вкладення графа, називається його числом черг[6][44][45].
Обчислювальна складність
ред.Визначення товщини книжкового вкладення є NP-складною задачею. Це випливає з факту, що знаходження гамільтонового циклу в максимальних планарних графах є NP-повною задачею. Товщина книжкового вкладення максимального планарного графа дорівнює двом і тоді, коли гамільтонів шлях існує. Тому визначення, що товщина книжкового вкладення заданого максимального планарного графа дорівнює двом також є NP-повною задачею[7].
Якщо порядок розташування вершин уздовж корінця за книжкового вкладення визначено, двосторінкове вкладення (якщо таке існує) можна знайти за лінійний час як варіант перевірки планарності для графа, отриманого розширенням заданого графа шляхом створення циклу, що з'єднує вершини уздовж корінця[13]. Унгер стверджував, що тристорінкове вкладення з певним порядком вершин може знайти за поліноміальний час, хоча в його описі цього результату відсутня низка істотних деталей[18]. Однак для графів, які вимагають чотири і більше сторінок, задача пошуку вкладення з найменшим можливим числом сторінок залишається NP-складною через еквівалентність NP-складній задачі розфарбовування колових графів, графів перетинів хорд кола. Якщо задано граф з фіксованим порядком вершин на корінці, розташування цих вершин у тому самому порядку на колі та подання ребер графа у вигляді відрізків дає набір хорд, що представляють граф . Можна тепер утворити коловий граф, що має хорди цієї діаграми як вершини, а пари хорд, що перетинаються, як ребра. Розфарбування колового графа дає розбиття ребер графа на підмножини, які можна намалювати без перетинів на одній сторінці. Таким чином, оптимальне розфарбування еквівалентне оптимальному книжковому вкладенню. Оскільки розфарбовування колового графа в чотири і більше кольорів є NP-складною задачею, і оскільки будь-який коловий граф можна утворити в такий спосіб із деякої задачі знаходження книжкового вкладення, знаходження оптимального книжкового вкладення є також NP-складною задачею[8][46][47]. Для фіксованого порядку вершин на корінці при двосторінковому вкладенні є NP-складною задачею мінімізація числа перетинів, якщо це число не дорівнює нулю[46].
Якщо порядок вершин на корінці невідомий, але розбиття ребер за сторінками встановлено, можна знайти 2-сторінкове вкладення (якщо таке існує) за лінійний час, застосувавши алгоритм, заснований на SPQR-деревах[48][49]. Однак, пошук 2-сторінкового вкладення є NP-повною задачею, якщо ні порядок вершин на корінці, ні розбиття ребер за сторінками не відомі. Пошук книжкового числа перетинів графа є також NP-складною задачею через NP-повноту задачі перевірки, чи є двосторінкове книжкове число перетинів нулем.
Задачу ізоморфізму підграфа, яка полягає у визначенні, чи обмежений у розмірі граф деякого виду як підграф більшого графа, можна розв'язати за лінійний час, якщо більший граф має обмежену товщину книжкового вкладення. Це істинне і для визначення, чи є граф деякого виду породженим підграфом більшого графа, або він має гомеоморфізм із більшим графом[50][51]. З тієї ж причини задача перевірки, чи задовольняє граф із обмеженою книжковою товщиною заданій формулі логіки первого порядка, розв'язна відносно фіксованого параметра[en][52].
Застосування
ред.Відмовостійкі мультипроцесорні обчислення
ред.Одним із основних приводів вивчення книжкового вкладення (за Чангом, Ляйтоном і Розенбергом[7]) є його використання в розробці НВІС для створення відмовостійких багатопроцесорних систем. У системі DIOGENES, яку розробили ці автори, процесори багатопроцесорної системи організовані в логічний ланцюжок, що відповідає корінцю книги (хоча вони не обов'язково розташовані на прямій физично на схемі). Комунікаційні зв'язки цих процесорів групуються в «пучки», які відповідають сторінкам книги і працюють подібно до стеків — з'єднання одного з процесорів із початком комунікаційної лінії штовхає вгору всі попередні з'єднання в пучку, а з'єднання іншого процесора з кінцем комунікаційної лінії з'єднує його з одним із нижніх процесорів пучка і штовхає решту вниз. Через таку стекову поведінку окремий пучок може обслуговувати набір комунікаційних ліній, які утворюють ребра окремої сторінки книжкового вкладення. За розташування зв'язків у такий спосіб, можна імплементувати широкий набір топологічних схем, у яких неважливо, який із процесорів дасть збій, доки досить багато процесорів залишаються в мережі. Мережеві топології, які можна організувати такою системою — це точно ті, книжкова товщина яких не перевищує числа пучків, які слід зробити доступними[7].
Стекове сортування
ред.Інше застосування, на яке вказали Чанг, Ляйтон і Розенберг[7], стосується сортування перестановок із використанням стеків. Кнут показав, що система, яка обробляє потік даних, заштовхуючи вхідні елементи в стек, а потім, у потрібний час, виштовхуючи їх у вихідний потік, може сортувати дані тоді й лише тоді, коли у вхідному порядку елементів немає перестановок із шаблоном[en] 231[53]. Відтоді з'явилося багато робіт щодо цієї та схожих задач сортування потоку даних загальнішими системами стеків та черг. У системі, яку розглядають Чанг, Ляйтон і Розенберг, кожен елемент вхідного потоку має бути вміщеним у один зі стеків. Після того, як усі дані буде вміщено в стеки, елементи виштовхуються із цих стеків (у відповідному порядку) у вихідний потік. Як зазначив Чанг та інші, така система може відсортувати задану перестановку тоді й лише тоді, коли деякий граф, отриманий із перестановки, має книжкове вкладення з фіксованим порядком вершин уздовж корінця і числом сторінок, що не перевищує числа стеків[7].
Керування рухом
ред.Як описує Кайнен[12], книжкове вкладення можна використати для опису фаз світлофорів на керованому перехресті. На перехресті вхідні та вихідні ряди руху (включно з кінцями пішохідних переходів та велосипедними лініями) можна подати як вершини графа, розташовані на корінці книжкового вкладення в порядку, що відповідає порядку входів/виходів руху через перехрестя (за годинниковою стрілкою). Шляхи через перехрестя, якими рухаються транспорт і пішоходи від точки входу до точки виходу, можна подати як ребра ненапрямленого графа. Наприклад, цей граф може мати ребро від вхідного ряду руху у вихідний ряд, що належить тому ж сегменту дороги, подаючи тим самим розворот, якщо розворот на перехресті дозволено. Задана підмножина таких ребер подає набір шляхів, якими може здійснюватися рух без перетинів, у тому й лише в тому випадку, коли підмножина не містить пари ребер, що перетинаються, які містяться на одній сторінці книжкового вкладення. Таким чином, книжкове вкладення графа описує розділення шляхів на підмножини, в яких рухи не перетинаються, і книжкова товщина цього графа (з фіксованим вкладенням на корінці) дає найменшу кількість різних фаз світлофора, необхідних для розкладу світлофора, які включають усі можливі шляхи через перехрестя[12]. Однак ця модель незастосовна до складніших систем регулювання руху, які не мають фіксованого розкладу.
Візуалізація графів
ред.Книжкове вкладення часто застосовують також для візуалізації мережевого потоку даних. Дві стандартні схеми візуалізації графів, дугові діаграми[10] та колові діаграми[11], можна розглядати як книжкові вкладення. Книжкове вкладення можна використати також для побудови кластерних схем[48], одночасних вкладень[54] та тривимірних малюнків графів[55].
Дугова діаграма[10] або лінійне вкладення[46] має вершини графа на прямій, а ребра графа малюються як півкола над і під цією прямою, іноді дозволяючи ребрам бути відрізками прямої. Такий стиль малювання відповідає книжковому вкладенню з однією сторінкою (якщо всі півкола лежать над прямою) або з двома сторінками (якщо використовуються обидві сторони від прямої), його введено спочатку як спосіб вивчення числа перетинів графів[56][57]. Планарні графи, що не мають двосторінкового книжкового вкладення, можна намалювати в подібний спосіб, дозволивши ребра подавати двома півколами над та під прямою лінією. Такі малюнки не є книжковими вкладеннями з погляду звичайного визначення та називаються топологічними книжковими вкладеннями[58]. Для будь-якого планарного графа завжди можна знайти таке вкладення, яке перетинає корінець не більше одного разу[59].
За іншого стилю малювання, вершини графа розташовуються на колі, а ребра малюються всередині або зовні кола[11]. Знову ж, розташування ребер усередині кола (наприклад, як відрізків) відповідає односторінковому книжковому вкладенню, тоді як розташування ребер по обидва боки від кола відповідає двосторінковому книжковому вкладенню[60].
Для односторінкових малюнків будь-якого стилю важливо зберігати кількість перетинів малою, щоб зменшити візуальний хаос малюнка. Мінімізація числа перетинів є NP-повною задачею[46], але її можна апроксимувати з відношенням , де — число вершин[61]. Мінімізація односторінкового чи двосторінкового числа перетинів розв'язна відносно фіксованого параметра[en], коли параметризується цикломатичним числом заданого графа[62]. Розроблялися також евристичні методи зменшення складності перетинів, засновані, наприклад, на акуратному порядку вставлення вершин і локальної оптимізації [11].
Двосторінкове книжкове вкладення з фіксованим розподілом ребер по сторінках можна подати як вид кластерної планарності[en], в якій заданий граф слід намалювати, розташувавши частини графа (дві підмножини ребер) так, щоб відобразити їх кластеризацію[48]. Двосторінкове книжкове вкладення використовують також для пошуку одночасного вкладення графів, за якого два графи задано на одній множині вершин, і потрібно знайти таке розташування вершин, щоб обидва графи малювалися планарно за допомогою прямих відрізків[54].
Книжкові вкладення, що мають понад дві сторінки, використовують для побудови тривимірних малюнків графів. Зокрема, Вуд використав побудову книжкових вкладень, що зберігають низький степінь кожної вершини всередині кожної сторінки, як метод вкладення графів у тривимірну ґратку малого об'єму[55].
Фолдинг РНК
ред.При вивченні того, як молекули РНК складаються при утворенні структури РНК, стандартний вигляд вторинної структури нуклеїнової кислоти[en] можна описати за допомогою діаграми як ланцюжок основ (послідовність РНК), намальованих уздовж прямої разом із набором дуг над лінією, які описують спарені основи структури. Тобто, хоча ця структура має складний тривимірний вигляд, її зв'язки (якщо вторинна структура існує) можна описати абстрактнішою структурою, односторінковим книжковим вкладенням. Однак не всі РНК поводяться так просто. Гаслінгер і Стадлер запропонували так звану «бівторинну структуру» для певних псевдовузлів РНК, які набувають вигляду двосторінкового книжкового вкладення — послідовність РНК знову малюється вздовж прямої, але спарені основи малюються як дуги над та під цією лінією. Для утворення вторинної структури граф повинен мати степінь, що не перевищує трьох — кожна основа може бути тільки в одному ребрі діаграми, а також у двох зв'язках із сусідніми основами в послідовності. Перевагою цього формулювання є те, що воно виключає структури, які фактично зв'язані в просторі, і що воно охоплює більшість відомих псевдовузлів РНК[13].
Оскільки порядок на корінці відомий зразу, існування вторинної структури для заданих спарених основ перевіряється безпосередньо. Задачу розподілу ребер за двома сторінками можна сформулювати як окремий випадок задачі виконуваності булевих формул у 2-кон'юнктивній нормальній формі[en] або як задачу перевірки двочастковості колового графа, вершинами якого є спарені основи, а ребра описують перетини між спареними основами[13]. Іншим і ефективнішим, як показали Хаслінгер і Стадлер[13], способом визначення, що бівторинна структура існує, є факт, що це трапляється в тому і лише в тому випадку, коли вхідний граф (граф, утворений з'єднанням основ у цикл у порядку їх слідування і додаванням спарених основ як ребер) є планарним[13]. Цей факт дозволяє розпізнати бівторинну структуру за лінійний час як окремий випадок перевірки планарності.
Блін, Фертін, Русу та Сіноквет використали зв'язок між вторинними структурами та книжковими вкладеннями як частину доведення NP-складності деяких задач порівняння вторинних структур РНК[63]. І якщо структура РНК скоріше третинна, ніж бівторинна, (тобто якщо потрібно більше двох сторінок на її діаграмі), то визначення числа сторінок знову ж NP-складна задача[64].
Теорія обчислювальної складності
ред.Паван, Теварі і Вінодсоандран використали книжкове вкладення для вивчення обчислювальної складності задачі досяжності в орієнтованих графах. Вони помітили, що задачу досяжності для двосторінкових орієнтованих графів можна розв'язати в однозначному логарифмічному просторі (аналозі детермінованої логарифмічної складності за пам'яттю задач класу UP[en]). Однак задача визначення досяжності для тристорінкових орієнтованих графів дає недетерміновану логарифмічну складність за пам'яттю. Отже, книжкове вкладення, схоже, тісно пов'язане з відмінностями між двома класами складності[65].
Існування експандерів зі сталим числом сторінок[43] є ключовим кроком для доведення, що немає підквадратичного за часом моделювання двострічкових недетермінованих машин Тюрінга за допомогою однострічкових недетермінованих машин[66].
Інші галузі математики
ред.Макензі та Овербей[14] вивчали застосування книжкової товщини в загальній алгебрі за допомогою графів, отриманих з дільників нуля скінченного локального кільця створенням вершини для кожного дільника нуля та ребра для кожної пари значень, добуток яких дорівнює нулю [14].
У серії статей Динніков[ru] вивчав топологічні книжкові вкладення вузлів і зачеплень, показуючи, що ці вкладення можна описати комбінаторною послідовністю символів і що топологічну еквівалентність двох зачеплень можна показати послідовністю локальних змін у вкладеннях[15][16].
Примітки
ред.- ↑ а б в г д е ж и к Bernhart, Kainen, 1979, с. 320—331.
- ↑ а б в г д Heath, 1987, с. 198—218.
- ↑ а б Shahrokhi et al, 1996, с. 413—424.
- ↑ а б в г Eppstein, 2001.
- ↑ а б в г Yannakakis, 1989, с. 36—67.
- ↑ а б в г д Nešetřil, Ossona de Mendez, 2012, с. 321—328.
- ↑ а б в г д е ж Chung et al, 1987, с. 33—58.
- ↑ а б Unger, 1988, с. 61—72.
- ↑ Arnold L. Rosenberg. Proceedings of the seventeenth Southeastern international conference on combinatorics, graph theory, and computing (Boca Raton, Fla., 1986). — 1986. — Т. 54. — С. 217–224. — (Congressus Numerantium).
- ↑ а б в Wattenberg, 2002, с. 111—116.
- ↑ а б в г Baur, Brandes, 2005, с. 332—343.
- ↑ а б в Kainen, 1990, с. 127—132.
- ↑ а б в г д е ж Haslinger et al, 1999, с. 437—467.
- ↑ а б в McKenzie, Overbay, 2010, с. 55—63.
- ↑ а б Dynnikov, 1999, с. 25—37, 96.
- ↑ а б Dynnikov, 2001, с. 243—283.
- ↑ а б Blankenship, Oporowski, 2009.
- ↑ а б Walter Unger. STACS 92: 9th Annual Symposium on Theoretical Aspects of Computer Science, Cachan, France, February 13–15, 1992, Proceedings. — Berlin : Springer, 1992. — Т. 577. — С. 389–400. — (Lecture Notes in Computer Science) — DOI:.
- ↑ а б в г д Dujmović, Wood, 2007, с. 641—670.
- ↑ а б в г Enomoto, Miyauchi, 1999, с. 337—341.
- ↑ а б Persinger, 1966, с. 169—173.
- ↑ а б Atneosen, 1968, с. 79.
- ↑ Gail H. Atneosen. One-dimensional n-leaved continua // Fundamenta Mathematicae. — 1972. — Т. 74, вип. 1. — С. 43–45..
- ↑ Paul C. Kainen. Graphs and Combinatorics (Proceedings of the Capital Conference on Graph Theory and Combinatorics at the George Washington University June 18–22, 1973) / Ruth A. Bari, Frank Harary. — 1974. — Т. 406. — С. 76–108. — (Lecture Notes in Mathematics).
- ↑ L. Taylor Ollmann. Proc. 4th Southeastern Conference on Combinatorics, Graph Theory and Computing / Frederick Hoffman, Roy B. Levow, Robert S. D. Thomas. — 1973. — Т. VIII. — С. 459. — (Congressus Numerantium).
- ↑ а б в Yannakakis, 1986, с. 104—108.
- ↑ T. C. Hales. Sphere packings. II // Discrete & Computational Geometry. — 1997. — Т. 18, вип. 2. — С. 135–149. — DOI:..
- ↑ В оригіналі — spine або back
- ↑ Elena Stöhr. A trade-off between page number and page width of book embeddings of graphs // Information and Computation. — 1988. — Т. 79, вип. 2. — С. 155–162. — DOI:..
- ↑ Elena Stöhr. The pagewidth of trivalent planar graphs // Discrete Mathematics. — 1991. — Т. 89, вип. 1. — С. 43–49. — DOI:..
- ↑ а б в г Blankenship, Oporowski, 1999.
- ↑ Hikoe Enomoto, Miki Shimabara Miyauchi, Katsuhiro Ota. Lower bounds for the number of edge-crossings over the spine in a topological book embedding of a graph // Discrete Applied Mathematics. — 1999. — Т. 92, вип. 2—3. — С. 149–155. — DOI:..
- ↑ Bernardo M. Ábrego, Oswin Aichholzer, Silvia Fernández-Merchant, Pedro Ramos, Gelasio Salazar. Proceedings of the 28th Annual Symposium on Computational Geometry (SCG'12). — ACM, New York, 2012. — С. 397–403. — DOI:
- ↑ Більше результатів щодо книжкової товщини повних двочасткових графів див. Etienne de Klerk, Dmitrii V. Pasechnik, Gelasio Salazar. Book drawings of complete bipartite graphs // Discrete Applied Mathematics. — 2014. — Т. 167. — С. 80–93. — DOI:..
- ↑ Toru Hasunuma, Yukio Shibata. Embedding de Bruijn, Kautz and shuffle-exchange networks in books // Discrete Applied Mathematics. — 1997. — Т. 78, вип. 1—3. — С. 103–116. — DOI:. Yuuki Tanaka, Yukio Shibata. On the pagenumber of the cube-connected cycles // Mathematics in Computer Science. — 2010. — Т. 3, вип. 1. — С. 109–117. — DOI:. Див. також Bojana Obrenić. Embedding de Bruijn and shuffle-exchange graphs in five pages // SIAM Journal on Discrete Mathematics. — 1993. — Т. 6, вип. 4. — С. 642–654. — DOI:..
- ↑ Bekos et al, 2014, с. 137—148.
- ↑ Lenny Heath. Proceedings of the 25th Annual Symposium on Foundations of Computer Science. — 1984. — С. 74–83. — DOI:
- ↑ Joseph L. Ganley, Lenwood S. Heath. The pagenumber of k-trees is O(k) // Discrete Applied Mathematics. — 2001. — Т. 109, вип. 3. — С. 215–221. — DOI:..
- ↑ Seth M. Malitz. Graphs with E edges have pagenumber O(√E) // Journal of Algorithms : журнал. — 1994. — Т. 17, вип. 1 (7). — С. 71–84. — DOI:.
- ↑ Seth M. Malitz. Genus g graphs have pagenumber O(√g) // Journal of Algorithms. — 1994. — Т. 17, вип. 1. — С. 85–109. — DOI:..
- ↑ R. Blankenship. Book Embeddings of Graphs. — Department of Mathematics, Louisiana State University, 2003. — (Ph.D. thesis). Як процитовано в Нешетрі.
- ↑ János Barát, Jiří Matoušek, David R. Wood. Bounded-degree graphs have arbitrarily large geometric thickness // Electronic Journal of Combinatorics. — 2006. — Т. 13, вип. 1. — С. R3..
- ↑ а б Vida Dujmović, Anastasios Sidiropoulos, David R. Wood. 3-Monotone Expanders. — 2015. — arXiv:1501.05020., покращення ранішого результату Jean Bourgain. Expanders and dimensional expansion // Comptes Rendus Mathématique. — 2009. — Т. 347, вип. 7—8. — С. 357–362. — DOI:.; Jean Bourgain, Amir Yehudayoff. Expansion in and monotone expanders // Geometric and Functional Analysis. — 2013. — Т. 23, вип. 1. — С. 1–41. — DOI:.. Див. також Zvi Gali, Ravi Kannan, Endre Szemerédi. On 3-pushdown graphs with large separators // Combinatorica. — 1989. — Т. 9, вип. 1. — С. 9–19. — DOI:.; Zeev Dvir, Avi Wigderson. Monotone expanders: constructions and applications // Theory of Computing. — 2010. — Т. 6. — С. 291–308. — DOI:.
- ↑ Lenwood S. Heath, Arnold L. Rosenberg. Laying out graphs using queues // SIAM Journal on Computing. — 1992. — Т. 21, вип. 5. — С. 927–958. — DOI:..
- ↑ Vida Dujmović, David R. Wood. On linear layouts of graphs // Discrete Mathematics & Theoretical Computer Science. — 2004. — Т. 6, вип. 2. — С. 339–357..
- ↑ а б в г Masuda et al, 1990, с. 124—127.
- ↑ M. R. Garey, D. S. Johnson, G. L. Miller, C. H. Papadimitriou. The complexity of coloring circular arcs and chords // SIAM Journal on Algebraic and Discrete Methods. — 1980. — Т. 1, вип. 2. — С. 216–227. — DOI:.
- ↑ а б в Hong, Nagamochi, 2009.
- ↑ Patrizio Angelini, Marco Di Bartolomeo, Giuseppe Di Battista. Graph Drawing: 20th International Symposium, GD 2012, Redmond, WA, USA, September 19–21, 2012, Revised Selected Papers. — Springer, 2013. — Т. 7704. — С. 79–89. — (Lecture Notes in Computer Science) — DOI:.
- ↑ Nešetřil, Ossona de Mendez, 2008, с. 777—791.
- ↑ Nešetřil, Ossona de Mendez, 2012, с. 401, Corollary 18.1.
- ↑ Nešetřil, Ossona de Mendez, 2012, с. 405, Theorem 18.7.
- ↑ Donald E. Knuth. The Art Of Computer Programming Vol. 1. — Boston : Addison-Wesley, 1968. — ISBN 0-201-89683-4..
- ↑ а б Angelini et al, 2012, с. 150—172.
- ↑ а б Wood, 2002, с. 312—327.
- ↑ Thomas L. Saaty. The minimum number of intersections in complete graphs // Proceedings of the National Academy of Sciences of the United States of America. — 1964. — Т. 52. — С. 688–690. — DOI:..
- ↑ T. A. J. Nicholson. Permutation procedure for minimising the number of crossings in a network // Proceedings of the Institution of Electrical Engineers. — 1968. — Т. 115. — С. 21–26. — DOI:..
- ↑ Miki Miyauchi. Topological book embedding of bipartite graphs // IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences. — 2006. — Vol. E89-A, iss. 5. — P. 1223–1226. — DOI:.
- ↑ Francesco Giordano, Giuseppe Liotta, Tamara Mchedlidze, Antonios Symvonis. Algorithms and Computation: 18th International Symposium, ISAAC 2007, Sendai, Japan, December 17–19, 2007, Proceedings. — Springer, 2007. — Т. 4835. — С. 172–183. — (Lecture Notes in Computer Science) — DOI:.
- ↑ Hongmei He, Ondrej Sykora. Proceedings of the Workshop on Information Technologies – Applications and Theory (ITAT), Slovakia, September 15–19, 2004. — 2004.
- ↑ Farhad Shahrokhi, Ondrej Sýkora, László A. Székely, Imrich Vrt'o. Graph-Theoretic Concepts in Computer Science: 20th International Workshop, WG '94, Herrsching, Germany, June 16–18, 1994, Proceedings. — Springer, 1995. — Т. 903. — С. 256–268. — (Lecture Notes in Computer Science) — DOI:.
- ↑ Michael J. Bannister, David Eppstein, Joseph A. Simons. Graph Drawing: 21st International Symposium, GD 2013, Bordeaux, France, September 23–25, 2013, Revised Selected Papers. — 2013. — Т. 8242. — С. 340–351. — (Lecture Notes in Computer Science) — DOI:.
- ↑ Guillaume Blin, Guillaume Fertin, Irena Rusu, Christine Sinoquet. Combinatorics, Algorithms, Probabilistic and Experimental Methodologies: First International Symposium, ESCAPE 2007, Hangzhou, China, April 7-9, 2007, Revised Selected Papers. — 2007. — Т. 4614. — С. 140–151. — (Lecture Notes in Computer Science) — DOI:.
- ↑ Peter Clote, Stefan Dobrev, Ivan Dotu, Evangelos Kranakis, Danny Krizanc, Jorge Urrutia. On the page number of RNA secondary structures with pseudoknots // Journal of Mathematical Biology. — 2012. — Т. 65, вип. 6–7. — С. 1337–1357. — DOI:..
- ↑ A. Pavan, Raghunath Tewari, N. V. Vinodchandran. On the power of unambiguity in log-space // Computational Complexity. — 2012. — Т. 21, вип. 4. — С. 643–670. — DOI:..
- ↑ Zvi Galil, Ravi Kannan, Endre Szemerédi. On nontrivial separators for k-page graphs and simulations by nondeterministic one-tape Turing machines // Journal of Computer and System Sciences. — 1989. — Т. 38, вип. 1. — С. 134–149. — DOI:..
Література
ред.- C. A. Persinger. Subsets of n-books in E3 // Pacific Journal of Mathematics. — 1966. — Т. 18. — С. 169–173. — DOI:.
- Gail Adele Atneosen. On the embeddability of compacta in n-books: intrinsic and extrinsic properties. — Michigan State University, 1968. — С. 79. — (Ph.D. thesis)
- Frank R. Bernhart, Paul C. Kainen. The book thickness of a graph // Journal of Combinatorial Theory. — 1979. — Т. 27, вип. 3. — С. 320–331. — (Series B). — DOI:.
- Mihalis Yannakakis. Proceedings of the 18th ACM Symposium on Theory of Computing (STOC '86). — 1986. — С. 104–108. — ISBN 0-89791-193-8. — DOI:
- Lenwood S. Heath. Embedding outerplanar graphs in small books // SIAM Journal on Algebraic and Discrete Methods. — 1987. — Т. 8, вип. 2. — С. 198–218. — DOI:.
- Fan R. K. Chung, Frank Thompson Leighton, Arnold L. Rosenberg. Embedding graphs in books: A layout problem with applications to VLSI design // SIAM Journal on Algebraic and Discrete Methods. — 1987. — Т. 8, вип. 1. — С. 33–58. — DOI:.
- Walter Unger. Proceedings of the 5th Symposium on Theoretical Aspects of Computer Science (STACS '88). — Springer-Verlag, 1988. — Т. 294. — С. 61–72. — (Lecture Notes in Computer Science) — DOI:
- Mihalis Yannakakis. Embedding planar graphs in four pages // Journal of Computer and System Sciences. — 1989. — Т. 38. — С. 36–67. — DOI:.
- Paul C. Kainen. Proceedings of the Twentieth Southeastern Conference on Combinatorics, Graph Theory, and Computing (Boca Raton, FL, 1989). — 1990. — Т. 71. — С. 127–132. — (Congressus Numerantium)
- Sumio Masuda, Kazuo Nakajima, Toshinobu Kashiwabara, Toshio Fujisawa. Crossing minimization in linear embeddings of graphs // IEEE Transactions on Computers. — 1990. — Т. 39, вип. 1. — С. 124–127. — DOI:.
- Farhad Shahrokhi, László A. Székely, Ondrej Sýkora, Imrich Vrťo. The book crossing number of a graph // Journal of Graph Theory. — 1996. — Т. 21, вип. 4. — С. 413–424. — DOI:.
- Hikoe Enomoto, Miki Shimabara Miyauchi. Embedding graphs into a three page book with O(M log N) crossings of edges over the spine // SIAM Journal on Discrete Mathematics. — 1999. — Т. 12, вип. 3. — С. 337–341. — DOI:.
- Christian Haslinger, Peter F. Stadler. RNA structures with pseudo-knots: Graph-theoretical, combinatorial, and statistical properties // Bulletin of Mathematical Biology. — 1999. — Т. 61, вип. 3. — С. 437–467. — DOI:.
- I. A. Dynnikov. Three-page approach to knot theory. Coding and local motions // Rossiĭskaya Akademiya Nauk. — 1999. — Т. 33, вип. 4. — С. 25–37, 96. — DOI:.
- Robin Blankenship, Bogdan Oporowski. Drawing Subdivisions Of Complete And Complete Bipartite Graphs On Books. — Department of Mathematics, Louisiana State University, 1999. — (Technical Report 1999-4)
- David Eppstein. Separating geometric thickness from book thickness. — 2001. — P. 20. — arXiv:math.CO/0109195.
- I. A. Dynnikov. A new way to represent links, one-dimensional formalism and untangling technology // Acta Applicandae Mathematicae. — 2001. — Т. 69, вип. 3. — С. 243–283. — DOI:.
- Martin M. Wattenberg. Proceedings of IEEE Symposium on Information Visualization (INFOVIS 2002). — 2002. — С. 110–116. — DOI:
- David R. Wood. Graph Drawing: 9th International Symposium, GD 2001, Vienna, Austria, September 23–26, 2001, Revised Papers. — Berlin : Springer, 2002. — Т. 2265. — С. 312–327. — (Lecture Notes in Computer Science) — DOI:
- Michael Baur, Ulrik Brandes. Graph-Theoretic Concepts in Computer Science: 30th International Workshop, WG 2004, Bad Honnef, Germany, June 21-23, 2004, Revised Papers / van Leeuwen. — Springer, 2005. — Т. 3353. — С. 332–343. — (Lecture Notes in Computer Science) — DOI:
- Vida Dujmović, David R. Wood. Graph treewidth and geometric thickness parameters // Discrete and Computational Geometry. — 2007. — Т. 37, вип. 4. — С. 641–670. — DOI:.
- Jaroslav Nešetřil, Patrice Ossona de Mendez. Grad and classes with bounded expansion. II. Algorithmic aspects // European Journal of Combinatorics. — 2008. — Т. 29, вип. 3. — С. 777–791. — DOI:.
- Robin Blankenship, Bogdan Oporowski. Book Thickness of Subdivisions / David Wood // Open Problem Garden : сайт. — 2009. — . — 01.
- Seok-Hee Hong, Hiroshi Nagamochi. Two-page book embedding and clustered graph planarity. — Technical report 2009-004. — Dept. of Applied Mathematics and Physics, University of Kyoto, Japan, 2009. — (Technical report)
- Thomas McKenzie, Shannon Overbay. Book embeddings and zero divisors // Ars Combinatoria. — 2010. — Т. 95. — С. 55–63.
- Jaroslav Nešetřil, Patrice Ossona de Mendez. Sparsity: Graphs, Structures, and Algorithms. — Springer, 2012. — Т. 28. — С. 321–328. — (Algorithms and Combinatorics) — ISBN 978-3-642-27874-7. — DOI:
- Patrizio Angelini, Giuseppe Di Battista, Fabrizio Frati, Maurizio Patrignani, Ignaz Rutter. Testing the simultaneous embeddability of two graphs whose intersection is a biconnected or a connected graph // Journal of Discrete Algorithms. — 2012. — Т. 14. — С. 150–172. — DOI:.
- Michael A. Bekos, Martin Gronemann, Chrysanthi N. Raftopoulou. Proceedings of the 31st Symposium on Theoretical Aspects of Computer Science. — 2014. — С. 137–148. — DOI:

