Метод Сімпсона
Метод Сімпсона є одним із методів чисельного інтегрування. Названий на честь британського математика Томаса Сімпсона (1710—1761).
Формула
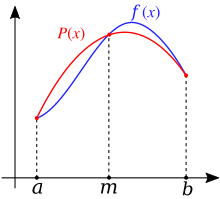
ред.Формулою Сімпсона називається інтеграл від інтерполяційного многочлена другого степеня на відрізку :
де , і — значення функції у відповідних точках .
Похибка
ред.При умові, що функція на відрізку має похідну четвертого порядку, похибка , дорівнює:
Зважаючи, що значення переважно не є відомим, для оцінки похибки використовується нерівність:
Виведення формули
ред.Формула Сімпсона може бути виведена за допомогою багатьох різних способів.
Квадратична інтерполяція
ред.Якщо замінити функцію квадратичним поліномом що приймає ті ж значення що й у точках a,b і m = (a+b) / 2. використавши інтерполяційну формулу Лагранжа, то одержимо формулу:
Після необхідних обчислень одержуємо:
Використання методів прямокутників і трапецій
ред.У цьому способі виведення використовуються метод прямокутників:
Похибки цих наближень дорівнюють
- і
відповідно. Звідси випливає, що аби позбутися третього степеня слід взяти для наближення величину
Однак таким чином одержується формула Сімпсона.
Метод невизначених коефіцієнтів
ред.Запишемо в загальному виді:
Коефіцієнти α, β і γ можуть бути знайдені з вимоги, що дане наближення є точним для всіх многочленів другого степеня. Таким чином знову ж одержується метод Сімпсона.
Ітераційна формула
ред.Для точнішого обчислення інтеграла проміжок розбивають на відрізків однакової довжини і застосовують формулу Сімпсона на кожному з них. Значення інтеграла є сумою для всіх відрізків.
- де величина кроку, а межі відрізків.
Загальну похибку при інтегруванні на відрізку з кроком визначають за формулою:
- .
При неможливості оцінити похибку за допомогою четвертої похідної можна використати слабшу оцінку:
- .
Приклади реалізації
ред.Реалізація на C#:
using System;
namespace NumericIntgeration
{
internal class Program
{
private delegate double Func(double x);
private static void Main()
{
const int n = 10000;
double result = SimpsonMethod(0.0, 2.0, n, x => x * Math.Exp(Math.Sqrt(x)));
Console.WriteLine("x = {0}", result);
Console.ReadKey();
}
private static double SimpsonMethod(double a, double b, int n, Func func)
{
double h = (b - a) / n;
double s = (func(a) + func(b)) * 0.5;
for (int i = 1; i <= n - 1; i++)
{
double xk = a + h * i; //xk
double xk1 = a + h * (i - 1); //Xk-1
s += func(xk) + 2 * func((xk1 + xk) / 2);
}
var x = a + h * n; //xk
var x1 = a + h * (n - 1); //Xk-1
s += 2 * func((x1 + x) / 2);
return s * h / 3.0;
}
}
}
Див. також
ред.Література
ред.- Формула парабол (формула Сімпсона) // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 450. — 594 с.
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2403 с.(укр.)