Панциклічний граф

Панциклі́чний граф — орієнтований або неорієнтований граф, який містить цикли всіх можливих довжин від трьох до числа вершин графа^[1]. Панциклічні графи є узагальненням гамільтонових графів, графів, які мають цикли найбільшої можливої довжини.

Визначення

Граф $G$ з $n$ вершинами є панциклічним, якщо для будь-якого $k$ в межах $3\leqslant k\leqslant n$ граф $G$ містить цикл довжини $k$ ^[1]. Граф є вершинно панциклічним, якщо для будь-якої вершини $v$ і будь-якого $k$ в тих самих межах граф містить цикл довжини $k$ , що містить вершину $v$ ^[2]. Схожим чином граф є реберно панциклічним, якщо для будь-якого ребра $e$ і для будь-якого $k$ в тих самих межах він містить цикл довжини $v$ , що містить ребро $e$ ^[2].

Двочастинний граф не може бути панциклічним, оскільки він не містить циклів будь-якої непарної довжини, але кажуть, що граф є біпанциклічним, якщо він містить цикли всіх парних довжин від 4 до $n$ ^[3].

Планарні графи

Максимальний зовніпланарний граф — це граф, утворений із простого многокутника на площині шляхом тріангуляції його внутрішності. Будь-який максимальний зовніпланарний граф є панциклічним, що можна показати індукцією. Зовнішня грань графа є циклом з n вершинами, а видалення будь-якого трикутника, з'єднаного із рештою графа тільки одним ребром (листок дерева, яке утворює двоїстий граф тріангуляції), утворює максимальний зовніпланарний граф з на одиницю меншим числом вершин, а за індукційним припущенням цей граф має всі цикли всіх довжин, що залишилися. Якщо приділяти більше уваги вибору трикутника для видалення, то ті самі аргументи показують строгіший результат, що будь-який максимальний зовніпланарний граф є вершинно панциклічним^[4]. Те ж саме істинне для графів, які мають максимальний зовніпланарний граф як кістяковий підграф, зокрема, для колеса.

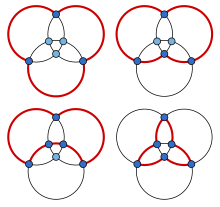
Максимальний планарний граф — це планарний граф, у якому всі грані, включно із зовнішньою, є трикутниками. Максимальний планарний граф є вершинно панциклічним тоді й лише тоді, коли він містить гамільтонів цикл^[5] — якщо він не гамільтонів, він безумовно не панциклічний, а якщо він гамільтонів, то внутрішність гамильтонового циклу утворює зовнішню межу максимального зовнішпланарного графа на тих самих вершинах і ребрах, до якої можна застосувати попередні аргументи для зовніпланарних графів^[6]. Наприклад, на малюнку вгорі показано панциклічність графа октаедра, гамільтонового максимального планарного графа з шістьма вершинами. Строгіше, з тих самих причин, якщо максимальний планарний граф має цикл довжини $k$ , то він має цикли всіх менших довжин^[7].

Майже панциклічний граф Халіна з циклами всіх довжин аж до n, за винятком довжини 8

Графи Халіна є планарними графами, утвореними з планарного малюнка дерева, яке має вершин степеня два, доданням циклу, що з'єднує листки дерева. Графи Халіна не обов'язково панциклічні, але вони майже панциклічні в тому сенсі, що відсутній цикл максимум однієї довжини. Довжина відсутнього циклу обов'язково парна. Якщо жодна зі внутрішніх вершин графа Халіна не має степеня три, то граф обов'язково панциклічний^[8].

1971 року помічено^[1], що багато класичних умов для існування гамільтонового циклу достатні також для панциклічності, тому припущено, що будь-який 4-зв'язний планарний граф панциклічний, але незабаром знайдено сімейство контрприкладів^[9].

Турніри

Турнір — це напрямлений граф з однією напрямленою дугою між будь-якою парою вершин. Інтуїтивно турнір можна використати для моделювання кругової системи малюванням дуги від переможця до переможеного для кожної гри в змаганні. Турнір називають сильно зв'язним або просто сильним тоді й лише тоді, коли його не можна розділити на дві непорожні підмножини $L$ і $W$ тих, хто програв і виграв, так, що будь-який учасник $W$ перемагає будь-якого учасника в $L$ ^[10]. Будь-який сильний турнір є панциклічним^[11] і вершинно панциклічним^[12]. Якщо турнір регулярний (будь-який учасник має таке ж число виграшів і програшів, що й інші учасники), то він є також реберно панциклічним^[13], однак сильні турніри з чотирма вершинами не можуть бути реберно панциклічними.

Графи з великим числом ребер

Теорема Мантеля стверджує, що будь-який неорієнтований граф із $n$ вершинами, що має принаймні $n^{2}/4$ ребер і не має кратних ребер і петель, або містить трикутник, або він є повним двочастинним графом $K_{n/2,n/2}$ . Цю теорему можна посилити — будь-який неорієнтований гамільтонів граф з не менш ніж $n^{2}/4$ ребрами або панциклічний, або це $K_{n/2,n/2}$ ^[1].

Існують гамільтонові орієнтовані графи з $n$ вершинами і з $n(n+1)/2-3$ дугами, які не є панциклічними, але будь-який гамільтонів орієнтований граф принаймні з $n(n+1)/2-1$ дугами панциклічний. Крім того, строго зв'язний граф з $n$ вершинами, в якому кожна вершина має степінь, не менший від $n$ (вхідні та вихідні дуги рахуються разом), або панциклічний, або є повним двочастинним графом^[14].

Степені графа

Для будь-якого графа $G$ його $k$ -й степінь графа $G^{k}$ визначається як граф на тій самій множині вершин, що має ребро між будь-якими двома вершинами, відстань між якими в $G$ не перевищує $k$ . Якщо $G$ вершинно 2-зв'язний, то за теоремою Фляйшнера $G^{2}$ є гамільтоновим графом. Твердження можна посилити: граф обов'язково буде вершинно панциклічним^[15]. Строгіше, якщо $G^{2}$ є гамільтоновим, він також і панциклічний^[16].

Обчислювальна складність

Перевірка графа на панциклічність є NP-повною задачею навіть для окремого випадку 3-зв'язних кубічних графів. NP-повною задачею є також перевірка графа на вершинну панциклічність навіть для окрмого випадку поліедральних графів^[17]. Також NP-повною задачею є перевірка квадрата графа на гамільтоновість, а тим самим і перевірка на панциклічність^[18].

Історія

Панциклічність уперше досліджували Харарі і Мозер у контексті турнірів^[19], а також Муун^[20] і Алпач^[13]. Назву поняттю панциклічності дав Бонді, який розширив поняття для неорієнтованих графів^[1].

Примітки

↑ ^а ^б ^в ^г ^д Bondy, 1971.
↑ ^а ^б Randerath, Schiermeyer, Tewes, Volkmann, 2002.
↑ Schmeichel, Mitchem, 1982.
↑ Li, Corneil, Mendelsohn, 2000, Proposition 2.5.
↑ Helden, 2007, Corollary 3.78.
↑ Bernhart, Kainen, 1979.
↑ Hakimi, Schmeichel, 1979.
↑ Skowrońska, 1985.
↑ Malkevitch, 1971.
↑ Harary, Moser, 1966, Corollary 5b.
↑ Harary, Moser, 1966, Theorem 7.
↑ Moon, 1966, Theorem 1.
↑ ^а ^б Alspach, 1967.
↑ Häggkvist, Thomassen, 1976, с. 20–40.
↑ Hobbs, (1976).
↑ Fleischner, 1976.
↑ Li, Corneil, Mendelsohn, 2000, Theorems 2.3 и 2.4.
↑ Underground, (1978).
↑ Harary, Moser, 1966.
↑ Moon, 1966.

Література

Brian Alspach. Cycles of each length in regular tournaments // Canadian Mathematical Bulletin. — 1967. — Т. 10, вип. 2 (3 січня). — С. 283—286..
Frank Bernhart, Paul C. Kainen. The book thickness of a graph // Journal of Combinatorial Theory, Series B. — 1979. — Т. 27, вип. 3 (3 січня). — С. 320—331. — DOI:10.1016/0095-8956(79)90021-2..
J. A. Bondy. Pancyclic graphs I // Journal of Combinatorial Theory, Series B. — 1971. — Т. 11, вип. 1 (3 січня). — С. 80—84. — DOI:10.1016/0095-8956(71)90016-5..
H. Fleischner. In the square of graphs, Hamiltonicity and pancyclicity, Hamiltonian connectedness and panconnectedness are equivalent concepts // Monatshefte für Mathematik. — 1976. — Т. 82, вип. 2 (3 січня). — С. 125—149. — DOI:10.1007/BF01305995..
Roland Häggkvist, Carsten Thomassen. On pancyclic digraphs // Journal of Combinatorial Theory, Series B. — 1976. — Т. 20, вип. 1 (3 січня). — DOI:10.1016/0095-8956(76)90063-0..
S. L. Hakimi, E. F. Schmeichel. On the number of cycles of length k in a maximal planar graph // Journal of Graph Theory. — 1979. — Т. 3 (3 січня). — С. 69—86. — DOI:10.1002/jgt.3190030108..
Frank Harary, Leo Moser. The theory of round robin tournaments // American Mathematical Monthly. — 1966. — Т. 73, вип. 3 (3 січня). — С. 231—246. — DOI:10.2307/2315334..
Guido Helden. Hamiltonicity of maximal planar graphs and planar triangulations. — Rheinisch-Westfälischen Technischen Hochschule Aachen, 2007. — (Dissertation).
Arthur M. Hobbs. The square of a block is vertex pancyclic // Journal of Combinatorial Theory. — 1976. — Т. 20, вип. 1 (3 січня). — С. 1—4. — (Series B). — DOI:10.1016/0095-8956(76)90061-7..
Ming-Chu Li, Derek G. Corneil, Eric Mendelsohn. Pancyclicity and NP-completeness in planar graphs // Discrete Applied Mathematics. — 2000. — Т. 98, вип. 3 (3 січня). — С. 219—225. — DOI:10.1016/S0166-218X(99)00163-8..
Joseph Malkevitch. Recent Trends in Graph Theory. — Springer-Verlag, 1971. — Т. 186. — С. 191—195. — (Lecture Notes in Mathematics) — DOI:10.1007/BFb0059437..
J. W. Moon. On subtournaments of a tournament // Canadian Mathematical Bulletin. — 1966. — Т. 9, вип. 3 (3 січня). — С. 297—301. — DOI:10.4153/CMB-1966-038-7..
Bert Randerath, Ingo Schiermeyer, Meike Tewes, Lutz Volkmann. Vertex pancyclic graphs // Discrete Applied Mathematics. — 2002. — Т. 120, вип. 1—3 (3 січня). — С. 219—237. — DOI:10.1016/S0166-218X(01)00292-X..
Edward Schmeichel, John Mitchem. Bipartite graphs with cycles of all even lengths // Journal of Graph Theory. — 1982. — Т. 6, вип. 4 (3 січня). — С. 429—439. — DOI:10.1002/jgt.3190060407..
Mirosława Skowrońska. Cycles in Graphs / Brian R. Alspach, Christopher D. Godsil. — Elsevier Science Publishers B.V, 1985. — Т. 27. — С. 179—194. — (Annals of Discrete Mathematics).
Paris Underground. On graphs with Hamiltonian squares // Discrete Mathematics. — 1978. — Т. 21, вип. 3 (3 січня). — С. 323. — DOI:10.1016/0012-365X(78)90164-4..

Посилання

Weisstein, Eric W. Панциклічний граф(англ.) на сайті Wolfram MathWorld.

[FOOTNOTEBondy1971-1] а ^б ^в ^г ^д Bondy, 1971.

[FOOTNOTERanderath,_Schiermeyer,_Tewes,_Volkmann2002-2] а ^б Randerath, Schiermeyer, Tewes, Volkmann, 2002.

[FOOTNOTESchmeichel,_Mitchem1982-3] Schmeichel, Mitchem, 1982.

[FOOTNOTELi,_Corneil,_Mendelsohn2000Proposition_2.5-4] Li, Corneil, Mendelsohn, 2000, Proposition 2.5.

[FOOTNOTEHelden2007Corollary_3.78-5] Helden, 2007, Corollary 3.78.

[FOOTNOTEBernhart,_Kainen1979-6] Bernhart, Kainen, 1979.

[FOOTNOTEHakimi,_Schmeichel1979-7] Hakimi, Schmeichel, 1979.

[FOOTNOTESkowrońska1985-8] Skowrońska, 1985.

[FOOTNOTEMalkevitch1971-9] Malkevitch, 1971.

[FOOTNOTEHarary,_Moser1966Corollary_5b-10] Harary, Moser, 1966, Corollary 5b.

[FOOTNOTEHarary,_Moser1966Theorem_7-11] Harary, Moser, 1966, Theorem 7.

[FOOTNOTEMoon1966Theorem_1-12] Moon, 1966, Theorem 1.

[FOOTNOTEAlspach1967-13] а ^б Alspach, 1967.

[FOOTNOTEHäggkvist,_Thomassen197620–40-14] Häggkvist, Thomassen, 1976, с. 20–40.

[FOOTNOTEHobbs1976-15] Hobbs, (1976).

[FOOTNOTEFleischner1976-16] Fleischner, 1976.

[FOOTNOTELi,_Corneil,_Mendelsohn2000Theorems_2.3_и_2.4-17] Li, Corneil, Mendelsohn, 2000, Theorems 2.3 и 2.4.

[FOOTNOTEUnderground1978-18] Underground, (1978).

[FOOTNOTEHarary,_Moser1966-19] Harary, Moser, 1966.

[FOOTNOTEMoon1966-20] Moon, 1966.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]