Парадокс берегової лінії
Парадокс берегової лінії — суперечливе спостереження в географічних науках, пов'язане з неможливістю точно визначити довжину лінії узбережжя через її фракталоподібні властивості. Перший задокументований опис цього феномену був зроблений Льюїсом Річардсоном[1]; згодом його було розширено Бенуа Мандельбротом[2].
| Парадокс берегової лінії | |
 | |
| Підтримується Вікіпроєктом |
Вікіпедія:Проєкт:Математика |
|---|---|
Довжина берегової лінії залежить від способу її вимірювання. Оскільки для ділянки суші можна виділити вигини будь-якого розміру, від сотень кілометрів до доль міліметра і менше, не можна очевидним чином підібрати розмір найменшого елементу, який має бути узятий для вимірювання. Отже, не можна однозначно визначити і периметр цієї ділянки. Існують різні математичні наближення для розвязання цієї задачі.
Історія розвитку парадоксу
ред.Незадовго до 1951 року Льюїс Фрай Річардсон в ході дослідження передбачуваного впливу довжини державних кордонів на імовірність початку військових конфліктів помітив наступне: формально сухопутний кордон Португалії з Іспанією дорівнює 987 км, проте в Португальській енциклопедії довжина кордону визначена як 1 214 км. Цей факт послужив відправною точкою для вивчення проблеми берегової лінії[3].
Основним методом оцінки довжини кордону або берегової лінії було накладення N рівних відрізків завдовжки / на карту або аерофотознімок за допомогою циркуля. Кожен кінець відрізку повинен належати вимірюваній лінії. Досліджуючи розбіжності в оцінці меж, Річардсон виявив те, що зараз називається ефектом Річардсона: масштаб вимірів обернено пропорційний до загальної довжини усіх відрізків. Тобто чим коротше використовувана лінійка, тим довше вимірювана межа. Таким чином, іспанські і португальські географи просто керувалися вимірами різних масштабів.
Найбільш вражаючим для Річардсона виявилося те, що коли величина l прагне до нуля, довжина узбережжя прагне до нескінченності. Спочатку Річардсон вважав, спираючись на геометрію Евкліда, що ця довжина досягне фіксованої величини, як це відбувається у випадку з правильними геометричними фігурами. Наприклад, периметр правильного багатокутника, вписаного в коло, наближається до довжини самого кола зі збільшенням числа сторін (і зменшенням довжини кожної сторони). У теорії геометричних вимірів така гладка крива, як коло, яке може бути приблизно представлене у вигляді невеликих відрізків із заданою межею, називається спрямлюваною кривою.
Понад десять років після завершення Річардсоном своєї роботи Мандельброт розробив нову гілку математики — фрактальну геометрію — для опису таких існуючих в природі комплексів, що не випрямляються, як нескінченна берегова лінія[4]. Його власне визначення фрактала як основи його дослідження таке[5]:
Я придумав слово фрактал, узявши за основу латинський прикметник fractus. Відповідне латинське дієслово frangere означає ламати: створювати нерегулярні фрагменти. Тому розумно, що, окрім «фрагментний», fractus також повинне означати і «нерегулярний».
Ключовою властивістю фракталів є самоподібність, що полягає в прояві однієї і тієї ж загальної фігури на будь-якому масштабі. Берегова лінія сприймається як чергування заток і мисів. Гіпотетично, якщо ця берегова лінія має властивість самоподібності, то незалежно від того, наскільки сильно масштабується та або інша частина, все одно проявляється аналогічна картина менших заток і мисів, накладена на більші затоки і миси, аж до піщинок. На таких масштабах берегова лінія виявляється ниткою, що миттєво змінюється, потенційно нескінченно, із стохастичним розташуванням заток і мисів. У таких умовах (на відміну від гладких кривих) Мандельброт стверджує: «Довжина берегової лінії виявляється недосяжним уявленням, що ковзає між пальцями тих, хто намагається його зрозуміти»[4].
Математична інтерпретація
ред.Поняття довжини походить від відстані Евкліда. У геометрії Евкліда пряма лінія є найкоротшою відстанню між двома точками. Геодезична лінія на поверхні сфери, що називається великим колом, вимірюється уздовж кривої, яка лежить в площині, що містить кінцеві точки шляху і центр сфери. Довжина кривої обчислюється складніше. При використанні лінійки довжину кривої можна приблизно обчислити, підсумовуючи довжини відрізків, що сполучають точки:
Використання усе більш коротких відрізків даватиме усе більш точне значення, що наближається до реального значення довжини дуги. Таке точне значення для нескінченно малих відстаней можна обчислити за допомогою математичного аналізу. Наступна анімація показує, наскільки гладкою може бути подібна крива з точним значенням довжини:
Проте не усі криві можуть бути виміряні подібним способом. Фрактал має різну складність залежно від масштабу, тому вимірювані значення довжин фракталів можуть непередбачувано змінюватися.
Крива Серпінського, де повторюється один і той же малюнок на дедалі менших масштабах, усе збільшується у довжину.
| |||||||||||
Мал. Крива Серпінського, що повторює один і той же малюнок на все менших масштабах, продовжує збільшуватися в довжині. Якщо розглядати ітерації в нескінченно подільному геометричному просторі, її довжина прагне до нескінченності. В той же час площа фігури, обмеженої цією кривою, прагне до певного значення — аналогічно тому, що площа острова вимірюється набагато легше, ніж довжина його берегової лінії.
Довжина «істинного фрактала» завжди прямує до нескінченності, так само як і довжини нескінченно малих вигинів берегової лінії підсумовуються до нескінченності[6]. Але це твердження засноване на припущенні про необмеженість простору, який, у свою чергу, навряд чи відбиває реальну концепцію простору і відстані на атомному рівні. Найменшою одиницею вимірювання довжини у Всесвіті вважається планківська довжина, набагато менша від розмірів атома.
Берегова лінія із властивістю самоподібності входить до «першої категорії фракталів, а саме є кривою з фрактальною розмірністю більше 1». Це останнє твердження є розширенням Мандельбротом думки Річардсона. Мандельброт так формулює ефект Ричардсона[7]:
де довжина берегової лінії L є функцією від одиниці вимірювання ε і апроксимується виразом з правої частини. F — константа, D — параметр Річардсона, залежний від самої берегової лінії (Річардсон не дав теоретичного пояснення цієї величини, проте Мандельброт визначив D як нецілочисельну форму розмірності Гаусдорфа, пізніше — фрактальної розмірності. Іншими словами, D — це практично виміряне значення «нерівності»). Перегрупувавши праву частину виразу, отримуємо:
де Fε- D має бути кількістю одиниць ε, необхідних для отримання L. Фрактальна розмірність — це число вимірювань об'єкта, використовуване для апроксимації фракталу: 0 — для точки, 1 — для лінії, 2 — для площадкових фігур. Оскільки ламана лінія, що вимірює довжину берега, не поширюється в одному напрямі і в той же час не є площею, значення D у виразі займає проміжне положення між 1 і 2 (для узбережжя зазвичай менше 1,5). Воно може бути інтерпретоване як товста лінія або смуга шириною 2ε. Більше «розбиті» узбережжя мають більше значення D і тим самим L виявляється довше при однакових ε. Мандельброт показав, що D не залежить від ε.
В цілому берегові лінії відрізняються від математичних фракталів, оскільки вони формуються з використанням численних дрібних деталей, що створюють моделі тільки статистично[8].
Парадокс на практиці
ред.У реальності на берегових лініях відсутні деталі менші 1 см. Це пов'язано з ерозією і іншими морськими явищами. У більшості місць мінімальний розмір значно більший. Тому модель нескінченного фрактала не підходить для берегових ліній.
З практичних міркувань вибирають мінімальний розмір деталей рівним порядку одиниць вимірювання. Так, якщо берегова лінія вимірюється в кілометрах, то невеликі зміни ліній, набагато менші одного кілометра, просто не беруться до уваги. Для вимірювання берегової лінії в сантиметрах мають бути розглянуті усі невеликі варіації розміром біля одного сантиметра. Проте на масштабах близько сантиметрів мають бути зроблені різні довільні нефрактальні припущення, наприклад, там, де гирло приєднується до моря, або в тих місцях, де мають бути проведені вимірювання на широких ваттах. Крім того, використання різних методів вимірювання для різних одиниць не дозволяє зробити перетворення цих одиниць за допомогою простого множення.
Граничні випадки парадоксу берегової лінії включають узбережжя з великим числом фіордів: це узбережжя Норвегії, Чилі, північно-західне узбережжя Північної Америки і інші. Від південного краю острова Ванкувер в північному напрямі до південного краю Південно-східної Аляски вигини узбережжя канадської провінції Британська Колумбія складають понад 10 % довжини канадської берегової лінії (з урахуванням усіх островів Канадського Арктичного архіпелагу) — 25725 км з 243042 км на лінійній відстані, рівній всього 965 км[9].
Див. також
ред.Література
ред.- Michael Frame, Benoit Mandelbrot, and Nial Neger. Coastlines. Fractals (англ.). yale.edu. Процитовано 13 лютого 2016.
- II.5 How long is the coast of Britain? // The Fractal Geometry of Nature. — Macmillan, 1983. — P. 25—33. — ISBN 978-0-7167-1186-5.
- How Much Length Do You Really Need? Ahhh, Shoreline Length That Is!. NOAA GeoZone Blog on Digital Coast (англ.). geozoneblog.wordpress.com. 26 березня 2012. Процитовано 13 лютого 2016.
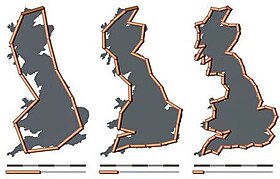
Парадокс вимірювання довжини берегової лінії Великої Британії
| |||||||||||
Відрізки по 100 км, довжина 2800 км
|
Відрізки по 50 км, довжина 3400 км
| ||||||||||
Примітки
ред.- ↑ Weisstein, Eric W. Coastline Paradox(англ.) на сайті Wolfram MathWorld.
- ↑ Mandelbrot, Benoit M.. The Fractal Geometry of Nature. — W. H. Freeman and Co., 1983. — P. 25—33. — ISBN 978-0-7167-1186-5.
- ↑ Ashford, Oliver M., Charnock, H., Drazin, P. G., Hunt, J. C. R. The Collected Papers of Lewis Fry Richardson / Ed. Ashford, Oliver M. — Cambridge University Press, 1993. — P. 45-46. — (Vol. 1. Meteorology and numerical analysis).
- ↑ а б Мандельброт (1983). — С. 28.
- ↑ Мандельброт (1983). — С. 1.
- ↑ Post & Eisen. — С. 550.
- ↑ Мандельброт (1983). — С. 29-31.
- ↑ Peitgen, H.-O., Jürgens, H., Saupe, D.. Irregular Shapes: Randomness in Fractal Constructions // Chaos and Fractals: New Frontiers of Science. — 2-е изд. — Springer, 2004. — P. 424. — ISBN 0-387-21823-8.
- ↑ Sebert, L. M., and M. R. Munro. 1972. Dimensions and Areas of Maps of the National Topographic System of Canada. Technical Report 72-1. Ottawa, Ont: Surveys and Mapping Branch, Department of Energy, Mines and Resources.