Многочлен
Многочленом, багаточленом або поліномом однієї змінної в математиці називається вираз вигляду
| Многочлен | |
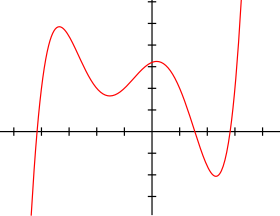 | |
| Формула |
|
|---|---|
| Позначення у формулі |
, і |
| Підтримується Вікіпроєктом |
Вікіпедія:Проєкт:Математика |
| | |

- Y = ,
де є сталими коефіцієнтами (константами), а — змінна.
Наприклад, , та , є многочленами, але та не є многочленами.
Многочленом від декількох змінних (багатовимірним многочленом) називається скінченна сума, в якій кожен з доданків є добутком скінченного числа цілих степенів змінних та константи:
- .
Многочлени є одним з найважливіших класів елементарних функцій.
Пов'язані терміни
ред.В многочлені доданки називаються його членами. Якщо , то називається старшим членом, а його степінь степенем многочлена. Степінь многочлена позначається . Член нульового степеня називається вільним членом.
Ще є нульовий многочлен (інколи пишуть , щоб підкреслити, що це не рівняння, а тотожність), який не має жодного члена, тому визначення степеня многочлена до нього застосувати не можна. Для зручності вважають, що степінь нульового многочлена дорівнює мінус нескінченності, .
Многочлен нульового степеня називається константою, першого степеня — лінійним, другого степеня — квадратичним, третього степеня — кубічним. Многочлени степеня більше нуля ми будемо називати неконстантними або нетривіальними.
Многочлен з одним членом називається одночленом, з двома членами — двочленом, з трьома — тричленом.
Наприклад, — кубічний тричлен з членами , і , причому — це старший член, а — вільний член.
Операції над многочленами
ред.- Сума многочленів є многочленом. Степінь суми многочленів менше або дорівнює максимуму степенів доданків.
- Добуток многочленів є многочленом. Степінь добутку многочленів дорівнює сумі степенів співмножників.
- Многочлени можна ділити з остачею: якщо — ненульовий многочлен, то будь-який многочлен можна представити у вигляді
- ,
де і — многочлени, причому .
Корінь многочлена
ред.Многочлен можна розглядати як функцію від змінної . Число називається коренем многочлена , якщо воно є коренем відповідної функції, тобто якщо . Це рівносильно умові «Многочлен ділиться на двочлен без остачі» (див. теорему Безу). Якщо ділиться на без остачі, то корінь називається кратним; якщо не ділиться, то простим. Кратністю кореня називається найбільше число , для якого ділиться на без остачі (таким чином, прості корені — це корені кратності 1).
Розкладання многочлена на нескоротні множники
ред.Якщо неконстантний многочлен можна представити у вигляді , де і — многочлени степеня не нижче першого, то кажуть, що розкладено на нетривіальні множники , . Якщо ж такого представлення не існує, многочлен називають нескоротним. Зрозуміло, що оскільки
- , і ,
то
- і .
Якщо якийсь з множників , можна розкласти на нетривіальні множники, то ми продовжимо процес розкладання допоки це можливо. Оскільки на кожному кроці степінь множників зменшується, цей процес є скінченним. Отже в результаті ми отримаємо представлення у вигляді
- ,
де многочлени є нескоротними. Таке представлення однозначно, з точністю до перестановки множників.
Основна теорема алгебри
ред.Комплексний многочлен степеня має рівно комплексних коренів, з урахуванням кратності.
Інакше кажучи, його можна розкласти на лінійних множників:
Таким чином, серед многочленів з комплексними коефіцієнтами нескоротними є лише лінійні многочлени.
Узагальнений многочлен
ред.Нехай — задана на система линійно незалежних функцій. Узагальненим многочленом будемо називати функцію
де — довільні дійсні числа (коэфіціенти узагальненого многочлена).
- Приклади
- , многочлен
- , тригонометричний многочлен
- , де функції Бесселя
Див. також
ред.Джерела
ред.- Завало С. Т. (1972). Елементи аналізу. Алгебра многочленів. Київ: Радянська школа. с. 462. (укр.)
- Розклад матричних многочленів на множники: монографія / П. С. Казімірський ; [відп. ред. Д. О. Супруненко] ; НАН України, Ін-т приклад. проблем механіки і математики ім. Я. С. Підстригача. — 2-ге вид., виправл. — Львів: ІППММ, 2015. — 282 с. : 1 арк. портр. — Бібліогр.: с. 274—280 (79 назв). — ISBN 978-966-02-7655-0
- Многочлен // Большая советская энциклопедия : в 30 т. / главн. ред. А. М. Прохоров. — 3-е изд. — М. : «Советская энциклопедия», 1969—1978. (рос.)
- Бурбаки Н. Алгебра ч.2 Многочлены и поля. Упорядоченные группы. — М. : Наука, 1965. — С. 300. — (Елементи математики)(рос.)
- Ван дер Варден Б. Л. Алгебра. — Москва : Наука, 1975. — 623 с. — ISBN 5-8114-0552-9.(рос.)
В іншому мовному розділі є повніша стаття Polynomial(англ.). Ви можете допомогти, розширивши поточну статтю за допомогою перекладу з англійської.
|










