Самодоповняльний граф
Самодоповняльний граф — це граф, ізоморфний своєму доповненню. Найпростіші нетривіальні самодоповняльні графи — це шлях, що складається з 4 вершин і цикл з 5 вершин.
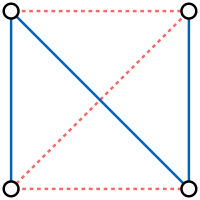

Приклади
ред.Будь-який граф Пелі є самодоповняльним[1]. Наприклад, 3 × 3 туровий граф (граф Пелі 9-го порядку) теж самодоповняльний, зважаючи на симетрію, що зберігає центральну вершину на місці, але обмінює ролі середніх точок по чотирьох краях і кутів ґратки[2]. Всі сильно регулярні самодоповняльні графи з менш ніж 37 вершинами є графами Пелі. Однак існують строго регулярні графи з 37, 41 і 49 вершинами, які не є графами Пелі[3].
Граф Радо є нескінченним самодоповняльним графом.
Властивості
ред.Самодоповняльний граф з n вершинами має рівно половину числа ребер повного графа, тобто n(n − 1)/4 ребер, і (якщо вершин більше однієї) його діаметр має бути або 2, або 3[1]. Оскільки n(n -1) має ділитися на 4, n має бути порівнянним з 0 або 1 за модулем 4. Наприклад, граф з 6 вершинами не може бути самодоповняльним.
Обчислювальна складність
ред.Задача перевірки, чи є два самодоповняльних графм ізоморфними і перевірка, чи є заданий граф самодоповняльним, еквівалентні за часом виконання загальній задачі перевірки ізоморфізму графів[en][4].
Примітки
ред.- ↑ а б Horst Sachs. Über selbstkomplementäre Graphen // Publicationes Mathematicae Debrecen. — 1962. — Т. 9 (25 січня). — С. 270—288.
- ↑ S. Shpectorov. Complementary l1-graphs // Discrete Mathematics. — 1998. — Т. 192, вип. 1-3 (25 січня). — С. 323—331. — DOI:.
- ↑ I. G. Rosenberg. Theory and practice of combinatorics. — North-Holland, 1982. — Т. 60 (25 січня). — С. 223—238.
- ↑ Marlene J. Colbourn, Charles J. Colbourn. Graph isomorphism and self-complementary graphs // SIGACT News. — 1978. — Т. 10, вип. 1 (25 січня). — С. 25—29. — DOI:.
Посилання
ред.- Weisstein, Eric W. Self-Complementary Graph(англ.) на сайті Wolfram MathWorld.