Серединний багатокутник
В геометрії серединний багатокутник багатокутника P — це багатокутник, вершини якого є серединами ребер P[1][2]. Його іноді називають багатокутником Каснера на честь Едварда Каснера[en], який «для стислості» назвав його «вписаним багатокутником»[3][4].

Приклади
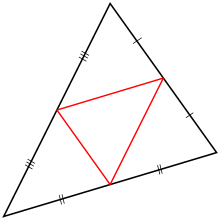
ред.Трикутник
ред.Серединний багатокутник трикутника називається серединним трикутником. Він має ті ж центроїд і медіани, що й вихідний трикутник. Периметр серединного трикутника дорівнює півпериметру вихідного трикутника, а площа становить одну чверть площі вихідного трикутника. Це можна довести використовуючи теорему про середину трикутників і формулу Герона. Ортоцентр серединного трикутника збігається з центром описаного кола вихідного трикутника.
Чотирикутник
ред.Серединний багатокутник чотирикутника є паралелограмом, який називається його паралелограмом Варіньона. Якщо чотирикутник простий, площа паралелограма дорівнює половині площі вихідного чотирикутника. Периметр паралелограма дорівнює сумі діагоналей вихідного чотирикутника.
Див. також
ред.Примітки
ред.- ↑ Gardner, 2006, с. 36.
- ↑ Gardner та Gritzmann, 1999, с. 92.
- ↑ Kasner, 1903, с. 59.
- ↑ Schoenberg, 1982, с. 91, 101.
Література
ред.- Gardner, Richard J. (2006), Geometric tomography, Encyclopedia of Mathematics and its Applications (англ.), т. 58 (вид. 2nd), Cambridge University Press
- Gardner, Richard J.; Gritzmann, Peter (1999), Uniqueness and Complexity in Discrete Tomography, у Herman, Gabor T.; Kuba, Attila (ред.), Discrete tomography: Foundations, Algorithms, and Applications (англ.), Springer, с. 85—114
- Kasner, Edward (March 1903), The Group Generated by Central Symmetries, with Application to Polygons, American Mathematical Monthly (англ.), 10 (3): 57—63, doi:10.2307/2968300, JSTOR 2968300
- Schoenberg, I. J. (1982), Mathematical time exposures (англ.), Mathematical Association of America, ISBN 0-88385-438-4
Подальше читання
ред.- Berlekamp, Elwyn R.; Gilbert, Edgar N.; Sinden, Frank W. (March 1965), A Polygon Problem, American Mathematical Monthly (англ.), 72 (3): 233—241, doi:10.2307/2313689, JSTOR 2313689
- Cadwell, J. H. (May 1953), A Property of Linear Cyclic Transformations, The Mathematical Gazette[en] (англ.), 37 (320): 85—89, doi:10.2307/3608930, JSTOR 3608930
- Clarke, Richard J. (March 1979), Sequences of Polygons, Mathematics Magazine[en] (англ.), 52 (2): 102—105, doi:10.2307/2689847, JSTOR 2689847
- Croft, Hallard T.; Falconer, K. J.; Guy, Richard K. (1991), B25. Sequences of polygons and polyhedra, Unsolved Problems in Geometry (англ.), Springer, с. 76—78
- Darboux, Gaston (1878), Sur un problème de géométrie élémentaire, Bulletin des sciences mathématiques et astronomiques, Série 2 (фр.), 2 (1): 298—304
- Gau, Y. David; Tartre, Lindsay A. (April 1994), The Sidesplitting Story of the Midpoint Polygon, Mathematics Teacher (англ.), 87 (4): 249—256, doi:10.5951/MT.87.4.0249
Посилання
ред.- Weisstein, Eric W. Midpoint Polygon(англ.) на сайті Wolfram MathWorld.