Симедіана

Симедіана ^{:стор.100} — чевіана трикутника, промінь якої симетричний променю медіани щодо бісектриси внутрішнього кута, проведеної з тієї ж вершини.

                     Медіани трикутника (перетинаються в центроїді G)                      Бісектриси внутрішніх кутів (перетинаються в центрі вписаного кола I)                      Симедіани (перетинаються в точці Лемуана L)

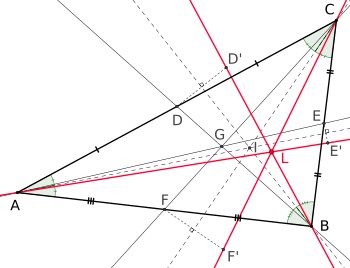
Тобто симедіана трикутника є відрізком, що ізогонально спряжений до його медіани.

Симедіана рівнобедреного трикутника, що проведена до його основи, збігається з його медіаною, бісектрисою та висотою.

Симедіана прямокутного трикутника, що проведена з вершини прямого кута на його гіпотенузу, збігається з його висотою. ^{:стор.100}

Властивості

• Довжину симедіани можна обрахувати за формулою: ^{:стор.107}

$$AS={\frac {bc}{b^{2}+c^{2}}}\cdot {\sqrt {2(b^{2}+c^{2})-a^{2}}}$$

де $a$ — сторона трикутника, протилежна вершині $A$, на яку проведено симедіану;
$b\,;\,c$ — сторони трикутника, що знаходяться обабіч симедіани.

• Відрізки, на які симедіана ділить протилежну сторону, пропорційні квадратам прилеглих сторін. ^{:стор.100 ; теорема}
• Симедіана трикутника є геометричним місцем точок, для яких відстані до сторін трикутника пропорційні довжинам цих сторін. ^{:стор.101 ; теорема 85}
• Симедіани трикутника перетинаються в одній точці, яка називається точкою Лемуана і позначається K або L . ^{:стор.102 ; теорема 86}
• Сума квадратів відстаней від точки на площині до сторін трикутника мінімальна, коли ця точка є точкою Лемуана.
• Відстані від точки Лемуана до сторін трикутника пропорційні довжинам сторін.
• Єдина точка, яка є центроїдом свого педального трикутника.
• Продовження симедіан проходять через відповідні вершини тангенціального трикутника.
• Антипаралелі трикутника діляться навпіл відповідними симедіанами. ^{:стор.104 ; теорема 88}
• Антипаралелі, що проведені через точку основи симедіани, рівні. Більш того, антипаралелі, що проходять через довільну точку симедіани, також рівні. ^{:стор.105 ; теорема 91}
  

Антипаралелі, що проходять через точку Лемуана (точку перетину симедіан), рівні і в точці перетину діляться навпіл.
Дотичні до описаного кола трикутника в двох його вершинах, перетинаються на симедіані, проведеної з третьої вершини.

Зовнішні симедіани трикутника

Відрізок дотичної до описаного кола трикутника, що проведена в його вершині до її точки перетину з протилежною стороною трикутника, називають зовнішньою симедіаною трикутника.

Її довжину можна обрахувати за формулою: ^{:стор.113, 114}

$$AD={\frac {abc}{b^{2}-c^{2}}}$$

Джерела

• Зетель С.И. Новая геометрия треугольника. — москва : учпедгиз, 1962. — С. 100-105.

Посилання

• Weisstein, Eric W. Symmedian(англ.) на сайті Wolfram MathWorld.
• Symmedian and Antiparallel на сайті cut-the-knot
• Symmedian and 2 Antiparallels на сайті cut-the-knot
• Symmedian and the Tangents на сайті cut-the-knot
• An interactive Java applet for the symmedian point
• Isogons and Isogonic Symmetry