Система відліку
Систе́ма ві́дліку — це фізичне тіло або набір тіл, відносно яких розглядається положення і рух інших тіл, система координат і синхронізовані годинники, що відраховують час. Одне з фундаментальних понять у фізиці. Якщо два тіла, з якими пов'язані різні системи відліку, рухаються одне відносно одного повільно, тривалість процесів і лінійні відстані між точками не залежать від того, яку з систем відліку ми оберемо, проте у випадку, якщо ці швидкості наближаються до швидкості світла, довжини і тривалості можуть змінюватися при переході з однієї системи в іншу.
| Система відліку | |
 | |
| Є об'єднанням | див. список:d |
|---|---|
| | |
Способи задання системи відліку
ред.Векторний спосіб
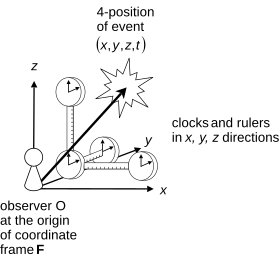
ред.Тут система відліку — це деяка фіксована точка простору О, прив'язана до деякого фізичного об'єкта, що називається тілом відліку. Положення іншої матеріальної точки в такому випадку задається вектором r, що починається в точці О і закінчується у точці, що нас цікавить. Такий вектор називають радіус-вектором[1].
Якщо за період вектор положення точки змінився з r0 на r1, то вектор називається вектором переміщення. А величина називається середнім вектором швидкості за час . Якщо , ця величина називається моментальною швидкістю: . Скалярна швидкість дорівнює довжині цього вектора. Аналогічно можна визначити прискорення як [2].
Координатний спосіб
ред.Тут система відліку включає, окрім початкової точки, деяку тривимірну систему координат, що може бути декартовою, косокутною або криволінійною. У такому разі положення точки задається трьома числами, що їх у декартових координатах позначають як x, y і z. Отже, кожне з записаних вище рівнянь розпадається на три, відповідно до окремих координат[3]. Наприклад:
Модуль швидкості обчислюється як:
Інерційні та неінерційні системи відліку
ред.Ньютонівська механіка
ред.Інерційна система відліку прив'язана до тіла, яке рухається без прискорення і без обертання. Згідно з першим законом Ньютона, таким чином рухається тіло, на яке не діють ніякі зовнішні сили. Інерційні системи відліку мають значні переваги перед неінерційними, оскільки у них закони механіки є значно простішими[4].
Існує нескінченна кількість систем відліку, що рухаються одна відносно одної рівномірно і прямолінійно у різних напрямках[5].
У неінерційних системах, що прив'язані до тіл, що рухаються з прискоренням, у рівняннях руху з'являються фіктивні сили або сили інерції, що не пов'язані ні з якою реальною взаємодією, а лише з вибором системи відліку[5]. Такими силами є, наприклад, відцентрова сила, сила Коріоліса, або сили, які ми відчуваємо у транспорті при розгоні або гальмуванні.
Хоча у ньютонівській механіці усі інерційні системи відліку є рівноправними (цей постулат називається принципом відносності Галілея), до 20 століття вважалося, що існує особлива, «справжня» система відліку, пов'язана з самим простором (або навіть з Богом). Таку система відліку називали абсолютною системою відліку. Зазвичай її прив'язували до ефіру — гіпотетичного середовища, що заповнює весь Всесвіт. Інший спосіб визначити абсолютну систему відліку запропонував Мах: він вважав, що густина матерії у Всесвіті зменшується при віддаленні від деякої точки, тобто, що у Всесвіту є центр мас. Систему відліку, пов'язану з ним, Мах і вважав абсолютною[6].
У 20 столітті, після створення спеціальної теорії відносності, стало зрозуміло, що концепт абсолютної системи відліку не має сенсу — її не існує, як не існує і ефіру. Нескінченність Всесвіту унеможливила і інтерпретацію Маха.
Загальна теорія відносності
ред.У ЗТВ вводиться поняття локально інерціальної системи відліку, що пов'язана з тілом, що знаходиться у стані вільного падіння. У такій системі відліку гравітацією можна повністю знехтувати, і усі тіла рухаються рівномірно і прямолінійно [7]. Проте такі властивості система буде мати лише якщо використовувати її на обмеженій ділянці простору-часу. Для будь-яких віддалених точок у гравітаційному полі, тіла що знаходяться у цих точках зазнають дії припливних сил. Розміри локально інерційної системи відліку залежать від необхідної точності вимірювань і кривини простору-часу. Наприклад, локально інерційна система відліку, прив'язана до тіла, що падає у гравітаційному полі Землі, може використовуватися в області простору-часу 100 м×100 м×100 м×3 с, якщо допустима похибка вимірювання перевищує 1,7 мм[8].
Перехід між системами відліку
ред.Перетворення Галілея
ред.У класичній механіці координати у двох системах, одна з яких рухається зі швидкістю відносно іншої перетворюються за наступним законом:
Ці рівняння називаються перетвореннями Галілея.
Відповідно, якщо тіло має швидкість і прискорення , у системі відліку , що рухається прямолінійно відносно іншої системи відліку зі швидкістю і прискоренням , швидкість тіла у системі дорівнюватиме[9]:
а прискорення
Тобто, наприклад, якщо ми заміряємо швидкість тіла у потязі, що їде, швидкість тіла відносно Землі дорівнює векторній сумі виміряної швидкості тіла і швидкості самого потягу.
У випадку, якщо система обертається з кутовою частотою відносно нерухомої (відносно першої системи) осі (обертова система відліку), то перетворення набувають вигляду (за умови, що початкові точки відліку обох систем збігаються, тобто, радіус-вектори усіх точок однакові в обох системах)[10]:
у рівнянні для перетворення прискорення другий доданок називається прискоренням Коріоліса а третій — відцентровим прискоренням[11].
Лінійні відстані між точками а також проміжки часу між подіями у класичній механіці ніяк не залежать від вибору системи відліку.
Перетворення Лоренца
ред.У релятивістській механіці, координати перетворюються за більш складним законом (при русі вздовж координати х зі швидкістю V)[12]:
де — швидкість світла, а — фактор Лоренца:
Тобто, у СТВ відстані між точками і тривалість часових інтервалів — не є інваріантами, а змінюються залежно від вибору системи відліку. Одночасність також є відносним поняттям — події, що відбулися в один і той самий момент у одній системі відліку, можуть відбутися в різні моменти часу, якщо перейти в іншу систему. Інваріантами є лише інтервали між двома подіями у просторі-часі[12]:
- ,
де — час між двома подіями а також відстань між ними у просторі
У випадку малих швидкостей перетворення Лоренца сходяться до перетворень Галілея (або ж, що те саме, перетворюються на них якщо прийняти швидкість світла нескінченною)[12].
Швидкості у цьому випадку перетворюються за законом[13]:
Якщо , то це рівняння буде виконуватися і при переході в будь-яку іншу систему відліку. Тобто, швидкість світла є однаковою для будь-якого спостерігача. Це твердження є одним з постулатів спеціальної теорії відносності[14].
Деякі особливі системи відліку
ред.Система відліку, пов'язана з Землею є зручною для багатьох повсякденних обчислень. Таку систему іноді називають геоцентричною. Вона може вважатися інерційною наближено, але якщо процеси, які досліджуються, мають велику протяжність у просторі або часі, обертання Землі має бути враховане. Першим продемонстрував це Леон Фуко у 1851 році. Він показав, що площина коливань довгого маятника (зараз таку систему називають маятником Фуко) поступово обертається з періодом 24 години. Зараз неінерційність геоцентричної системи відліку враховується в артилерії, ракетобудівництві, гіроскопічній техніці[15].
Для таких обчислень за інерційну приймають систему відліку, пов'язану з "нерухомими зірками" — за опорні точки для координатних осей приймаються три зорі[15]. У астрономії при використанні такої системи початок координат прив'язують до Сонця. Така система відліку називається геліоцентричною, і є інерційною з дуже великою точністю.
Для опису зіткнення двох тіл зручною є система, прив'язана до центру мас цих двох тіл.
Див. також
ред.Примітки
ред.- ↑ Иродов, 1985, с. 10.
- ↑ Иродов, 1985, с. 11.
- ↑ Иродов, 1985, с. 13.
- ↑ Иродов, 1985, с. 34.
- ↑ а б Иродов, 1985, с. 35.
- ↑ Юкава, 1981, с. 41.
- ↑ Мизнер,Торн,Уилер, 1977, с. 46.
- ↑ Мизнер,Торн,Уилер, 1977, с. 67.
- ↑ Иродов, 1985, с. 25.
- ↑ Иродов, 1985, с. 26.
- ↑ Иродов, 1985, с. 27.
- ↑ а б в Иродов, 1985, с. 192.
- ↑ Иродов, 1985, с. 199.
- ↑ Иродов, 1985, с. 200.
- ↑ а б Курс теоретической механики(рос.)
Література
ред.- Иродов И.Е. Основные законы механики. — 3. — М. : «Высшая школа», 1985. — 248 с.
- Юкава Х. Лекции по физике. — М. : Энергоиздат, 1981. — 128 с.
- Ч.Мизнер, К.Торн, Дж.Уилер. Гравитация. — М. : Мир, 1977. — Т. 2. — 480 с.