Теорема Паскаля
Теорема Паскаля — теорема проєктивної геометрії, яка свідчить, що
|
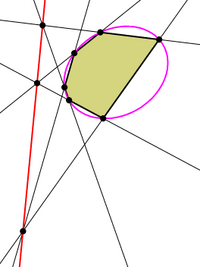
Якщо шестикутник вписаний в коло або будь-який інший конічний перетин (еліпс, параболу, гіперболу, навіть пару прямих), то точки перетину трьох пар протилежних сторін лежать на одній прямій. |
Теорема Паскаля двоїста до теореми Бріаншона.
Історія
ред.Вперше сформульована і доведена Блезом Паскалем у 16 років як узагальнення теореми Паппа. Цю теорему Паскаль взяв за основу свого трактату про конічні перетини. Сам трактат пропав і відомий лише його короткий зміст з листа Лейбніца, який під час свого перебування в Парижі мав його у своїх руках, і короткий виклад основних теорем цього трактату, складений самим Паскалем (Есе про конічні перетини).
Про доведення
ред.- Одне з доведень базується на підрахунку подвійних відношень.
- Ще одне доведення ґрунтується на послідовному застосуванні теореми Менелая.
- Проєктивним перетворенням можна перевести описану коніку в коло, при цьому умова теореми збережеться. Для кола теорема може бути доведена з існування ізогонального спряження.
- У разі опуклого багатокутника, вписаного в коло, можна здійснити проєктивне перетворення, що залишає коло на місці, а пряму, що проходить через точки перетину двох пар протилежних сторін відвести на нескінченність. У цьому випадку твердження теореми стане очевидним.
Застосування
ред.- Дозволяє будувати конічний перетин по п'яти точках як геометричне місце точок відповідних шостій точці шестикутника в конфігурації.
Варіації і узагальнення
ред.Теорема правильна і в тому випадку, коли дві або навіть три сусідніх вершини збігаються (але не більше ніж по дві в одній точці).
У цьому випадку як пряма, що проходить через дві вершини, що збігаються, приймається дотична до лінії в цій точці.
Зокрема:
|
Дотична до лінії 2-го порядку, проведена в одній з вершин вписаного п'ятикутника, перетинається зі стороною, протилежної цій вершині, в точці, яка лежить на прямій, що проходить через точки перетину інших пар несуміжних сторін цього п'ятикутника. |
|
Якщо ABCD — чотирикутник, вписаний в лінію 2-го порядку, то точки перетину дотичних в вершинах С і D відповідно зі сторонами AD і ВС і точка перетину прямих А В і CD лежать на одній прямій. |
|
Точки перетину дотичних в вершинах трикутника, вписаного в лінію 2-го порядку, з протилежними сторонами лежать на одній прямій. |
Ця пряма називається прямою Паскаля даного трикутника.
У 1847 з'явилося узагальнення теореми Паскаля, зроблене Мебіусом, яке звучить так:
|
Якщо багатокутник з сторонами вписаний в конічний перетин і протилежні його сторони продовжені таким чином, щоб перетнутися в точці, то якщо цих точок лежать на прямій, остання точка теж буде лежати на цій прямій. |
Теорема Кіркмана:
|
Нехай точки , , , , та лежать на одному конічному перетині. Тоді прямі Паскаля шестикутників , та перетинаються в одній точці. |
Посилання
ред.- Блез Паскаль. Опыт о конических сечениях с приложением письма Лейбница к Э. Перье. Перевод и комментарии Г. И. Игнациуса. // Историко-математические исследования. Выпуск XIV.
- Шаль. Исторический обзор происхождения и развития геометрических методов. Гл. 2, § 16-19. М., 1883.
- Р.Курант, Г.Роббинс, Что такое математика? [Архівовано 13 грудня 2012 у Wayback Machine.] Глава IV, § 8.4.
- Живые чертежи (на Java)
- Pascal's theorem [Архівовано 12 травня 2014 у Wayback Machine.] на Cut the knot [Архівовано 13 травня 2014 у Wayback Machine.]
- Pascal's theorem
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 76-78. — ISBN 5-94057-170-0