Трига́мма-фу́нкція в математиці є другою з полігамма-функцій. Її позначають  і визначають як
і визначають як
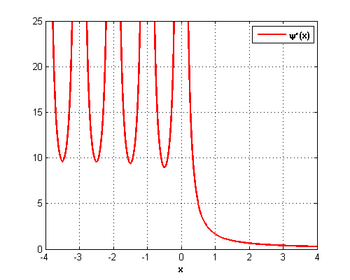 Тригамма-функція дійсного аргументу x
Тригамма-функція дійсного аргументу x

де  — гамма-функція[1]. З цього визначення випливає, що
— гамма-функція[1]. З цього визначення випливає, що

де  — дигамма-функція (перша з полігамма-функцій)[2].
— дигамма-функція (перша з полігамма-функцій)[2].
Тригамма-функцію можна також визначити через суму такого ряду:

звідки видно, що вона є окремим випадком дзета-функції Гурвіца,

Ці формули істинні, коли  (у зазначених точках функція
(у зазначених точках функція  має квадратичні сингулярності, див. графік функції).
має квадратичні сингулярності, див. графік функції).
Існують також інші позначення для  , використовувані в літературі:
, використовувані в літературі:

Іноді термін «тригамма-функція» застосовують для функції  [1].
[1].
Використовуючи подання у вигляді ряду, а також формулу для суми членів геометричної прогресії, можна отримати таке подвійне інтегральне подання:
-
За допомогою інтегрування за частинами виходить таке одинарне подання:
-
Використовується також інше подання, яке можна отримати з попереднього заміною x = e—t:
-
Тригамма-функція задовольняє рекурентне співвідношення[2]
-
а також формулу доповнення
-
Для тригамма-функції кратного аргументу існує така властивість[2]:
-
Наведемо також асимптотичний розклад із використанням чисел Бернуллі:
-
Нижче наведено часткові значення тригамма-функції:
-
-
-
-
-
-
де G — стала Каталана, а — функція Клаузена, пов'язана з уявною частиною дилогарифма через
-
Використовуючи формулу кратного аргументу і формулу доповнення, a також зв'язок з функцією Клаузена[3][4], маємо:
-
-
-
-
-
-
Для значень за межами інтервалу можна використати рекурентне співвідношення, наведене вище. Наприклад,
-
-
-
- ↑ а б Eric W. Weisstein Тригамма-функція(англ.) на сайті Wolfram MathWorld.
- ↑ а б в Eric W. Weisstein Полігамма-функція(англ.) на сайті Wolfram MathWorld.
- ↑ C.C. Grosjean, Formulae concerning the computation of the Clausen integral , J. Comp. Appl. Math. 11 (1984) 331—342
- ↑ P.J. de Doelder, On the Clausen integral and a related integral, J. Comp. Appl. Math. 11 (1984) 325—330










