Узагальнений чотирикутник
Узагальнений чотирикутник — це структура інцидентності, головна властивість якої — відсутність трикутників (однак структура містить багато чотирикутників). Узагальнений чотирикутник є за визначенням полярним простором[en] рангу два. Узагальнені чотирикутники є узагальненими многокутниками з n = 4 і майже 2n-кутниками з n = 2. Вони є також точно частковими геометріями pg(s,t, α) з α = 1.
Визначення
ред.Узагальнений чотирикутник — це структура інцидентності (P,B, I), де — відношення інцидентності, що задовольняє певним аксіомам. Елементи P за визначенням є вершинами (точками) узагальненого чотирикутника, елементи B — прямими. Аксіоми такі:
- Існує число s (s ≥ 1), таке, що на будь-якій прямій є рівно s+1 точка. Існує максимум одна точка на двох різних прямих.
- Існує число t (t ≥ 1), таке, що через будь-яку точку проходить рівно t + 1 пряма. Існує максимум одна пряма через дві різні точки.
- Для будь-якої точки p, що не лежить на прямій L, існує єдина пряма M і єдина точка q, такі, що p лежить на M, а q лежить на M і L.
Пара чисел є параметрами узагальненого чотирикутника. Параметри можуть бути нескінченними. Якщо або число s, або t дорівнює одиниці, узагальнений чотирикутник називається тривіальним. Наприклад, ґратка 3x3 з P = {1,2,3,4,5,6,7,8,9} і B = {123, 456, 789, 147, 258, 369} є тривіальним узагальненим чотирикутником з s = 2 і t = 1. Узагальнений чотирикутник з параметрами часто позначають як (від англ. Generalized Quadrangle).
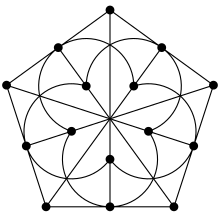
Найменший нетривіальний узагальнений чотирикутник — , подання якого 1973 року Стен Пейн назвав «серветкою».
Властивості
ред.Графи
ред.Є два цікавих графи, які можна отримати з узагальненого чотирикутника.
- Граф колінеарності, що містить усі точки узагальненого чотирикутника як вершини, в якому колінеарні точки з'єднані ребром. Цей граф є сильно регулярним графом з параметрами , де — порядок чотирикутника.
- Граф інцидентності, вершинами якого є всі точки і прямі узагальненого чотирикутника і дві вершини суміжні, якщо одна вершина відповідає прямій, а інша — точці на цій прямій. Граф інцидентності узагальненого чотирикутника зв'язний і є двочастковим графом з діаметр чотири і обхват вісім. Таким чином, узагальнений чотирикутник є прикладом клітина. Графи інцидентності конфігурацій в даний час називають графами Леві, однак вихідний граф Леві був графом інцидентності узагальненого чотирикутника .
Двоїстість
ред.Якщо (P,B, I) — узагальнений чотирикутник із параметрами (s,t), тоді (B,P,I−1) також є узагальненим чотирикутником (тут I−1 означає обернене відношення інцидентності). Цей чотирикутник називають двоїстим узагальненим чотирикутником. Його параметрами буде пара (t,s). Навіть при s = t двоїста структура не обов'язково ізоморфна початковій структурі.
Узагальнені чотирикутники з розміром прямих 3
ред.Існує рівно п'ять (допускається виродження) узагальнених чотирикутників, у яких кожна пряма має три інцидентні їй точки:
- чотирикутник з порожньою множиною прямих
- чотирикутник, у якому всі прямі проходять через фіксовану точку, що відповідає вітряку Wd(3,n)
- ґратка розміром 3x3
- чотирикутник
- узагальнений чотирикутник
Ці п'ять чотирикутників відповідають п'яти системам коренів у ADE класах An, Dn, E6, E7 і E8, тобто однонитковим системам коренів (це означає, що в діаграмах Динкіна елементи не мають кратних зв'язків)[1][2].
Класичні узагальнені чотирикутники
ред.Якщо розглядати різні види полярних просторів[en] рангу щонайменше три і екстраполювати їх на ранг 2, можна виявити ці (скінченні) узагальнені чотирикутники:
- Гіперболічна поверхня другого порядку (квадрика) , параболічна квадрика і еліптична квадрика є єдиними можливими квадриками в проєктивних просторах над скінченними полями з проєктивним індексом 1. Параметри цих квадрик:
- (це просто ґратка)
- Ермітів многовид має проєктивний індекс 1 тоді і тільки тоді, коли N дорівнює 3 або 4. Ми маємо:
- Симплектична полярність в має максимальний ізотропний підпростір розмірності 1 тоді й лише тоді, коли . Тут ми маємо узагальнений чотирикутник , з параметрами .
Узагальнений чотирикутник, похідний від завжди ізоморфний двоїстій структурі до , обидві структури самодвоїсті, а тому ізоморфні одна одній тоді й лише тоді, коли парне.
Некласичні приклади
ред.- Нехай O — гіперовал[en] в з q, рівним парному степеню простого числа, і вкладення цієї проєктивної (дезаргової) площині в . Тепер розглянемо структуру інцидентності , в якій усі точки є точками, що не лежать на . Прямі цієї структури — це точки, що не лежать на і перетинають в точці O, а інцидентність визначається природним чином. Це (q-1,q+1)-узагальнений чотирикутник.
- Нехай q — степінь простого числа (непарний або парний). Розглянемо симплектичну полярність в . Виберемо випадкову точку p і визначимо . Нехай прямими нашої структури інцидентності будуть усі абсолютні прямі[3], що не лежать на , разом з усіма прямими, що проходять через точку p, але не лежать на , а точками — всі точки , що не лежать на . Відношенням інцидентності буде природна інцидентність. Ми отримали знову (q—1,q+1)-узагальнений чотирикутник.
Обмеження на параметри
ред.Для ґраток і двоїстих ґраток для будь-якого цілого числа z, z ≥ 1 є узагальнені чотирикутники з параметрами (1,z) і (z,1). Крім цього випадку, виявляються допустимими лише такі параметри (тут q — довільний степінь простого числа):
- і
- і
- і
Примітка
ред.- ↑ Cameron, Goethals, Seidel, Shult, 1976, с. 305-327.
- ↑ Brouwer.
- ↑ Нехай простір має полярність (відображення точок у прямі порядку два зі збереженням інцидентності). У цьому випадку точка може лежати на своєму образі (на прямій), але це не обов'язково. Точка є абсолютною, якщо лежить на своєму образі, а пряма є абсолютною, якщо проходить через свій образ (точку).
Література
ред.- Payne S. E., Thas J. A. Finite generalized quadrangles. — Boston, MA : Pitman (Advanced Publishing Program), 1984. — Т. 110. — С. vi+312. — (Research Notes in Mathematics) — ISBN 0-273-08655-3.
- Payne S. E., Thas J. A. Finite generalized quadrangles. — European Mathematical Society, 2009. — (EMS Series of Lectures in Mathematics) — ISBN 978-3-03719-066-1.
- Cameron P.J., Goethals J.M., Seidel J.J, Shult E. E. Line graphs, root systems and elliptic geometry // Journal of Algebra. — Academic Press, 1976. — Т. 43, вип. 1 (29 грудня).
- Brouwer A.E. Algebra and Geometry (PDF).
{{cite web}}: Проігноровано невідомий параметр|description=(довідка)
