Умови Ренкіна — Гюгоніо
Умови Ренкіна — Гюгоніо — рівняння в гідроаеродинаміці, які описують зв'язок між станами по обидва боки ударної хвилі або хвилі горіння (дефлаграція чи детонація) в одновимірному потоці речовини або для одновимірної деформації твердих тіл. Вони названі на честь шотландського інженера й фізика Вільяма Джона Ренкіна[1] та французького інженера П'єра Анрі Гюгоніо[2][3].
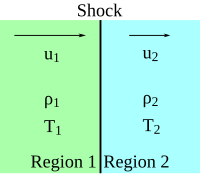
Основна ідея умов стрибка полягає в тому, щоб розглянути, що відбувається з речовиною, коли вона зазнає швидких змін. Розгляньмо, наприклад, введення поршня в трубу, наповнену газом, у якому не відбувається жодних хімічних перетворень. Збурення поширюється через речовину дещо швидше, ніж швидкість звуку, — з надзвуковою швидкістю, тому це ударна хвиля, і речовина за ударною хвилею ще не має інформації про це збурення. У системі відліку, що рухається разом із хвилею, атоми або молекули, врізаються в ударний фронт із надзвуковою швидкістю. На мікроскопічному рівні вони зазнають зіткнень у масштабі середньої довжини вільного пробігу, поки не зупиняться в потоці після ударного фронту (але рухаючись у системі відліку хвилі або трубки). Об'ємна передача кінетичної енергії нагріває потік після ударного фронту. Оскільки середня довжина вільного пробігу вважається незначною порівняно з усіма іншими масштабами задачі, ударний фронт є, по суті, гідродинамічним розривом. Тоді умови стрибка встановлюють зв'язок властивостей потоку до та після ударного фронту, заснований виключно на збереженні маси, імпульсу та енергії. Ці умови справедливі, навіть якщо товщина ударний фронт має суттєву товщину. Узагальненням такого прикладу нереагуючої ударної хвилі є реагуючі потоки, де фронт горіння (або детонації, або дефлаграції) може бути в першому наближенні змодельований як розрив.
Основні рівняння
ред.У системі координат, яка рухається разом із розривом, умови Ренкіна — Гюгоніо можна записати так[4]:
- збереження маси: ,
- збереження імпульсу: ,
- збереження енергії: ,
де m — розхід маси на одиницю площі, ρ1 і ρ2 — густина речовини перед і після хвилі, u1 і u2 — швидкість речовини перед і після хвилі, p1 і p2 — тиск, а h1 і h2 — питомі (на одиницю маси) ентальпії в цих двох областях. Якщо, крім того, у потоці відбуваються хімічні перетворення, то треба додатково додати рівняння збереження окремих компонентів,
- збереження компонентів:
щоб уникнути розриву на фронті. Тут, — швидкість виробництва i-ї речовини на одиницю маси, а N — загальна кількість речовин, що беруть участь у реакції.
Поєднання законів збереження маси та імпульсу дає
- ,
що визначає пряму лінію, відому як лінія Міхельсона–Релея, названу на Володимира Міхельсона і лорда Релея, яка має негативний нахил (оскільки завжди додатне) на площині [5]. Скориставшись рівняннями Ренкіна — Гюгоніо для збереження маси та імпульсу, щоб виключити u1 та u2, рівняння збереження енергії можна виразити у вигляді рівняння Гюгоніо:
- .
Значення, обернене густині, можна виразити як питомий об'єм, . Водночас необхідно вказати зв'язок між рівняннями стану вище й нижче за течією,
де є масовою часткою виду. Нарешті, припускаємо, що нам відоме калориметричне рівняння стану, тобто зв'язок між ентальпією та рештою параметрів , тоді
- .
Для спрощення рівнянь Ренкіна — Гюгоніо роблять наступні припущення. Вважають, що суміш підкоряється закону ідеального газу, тоді співвідношення між рівнянням стану нижче та вище за течією можна записати як
- ,
де — універсальна газова стала, а середня молекулярна маса вважається сталою (інакше залежить від масової частки всіх компонентів). Якщо припустити, що питома теплоємність при постійному тиску також постійна по всій хвилі, зміну ентальпії (калориметричне рівняння стану) можна просто записати як
- ,
де перший член у наведеному вище виразі позначає кількість тепла, що виділяється хвилею на одиницю маси суміші вище за течією, а другий член позначає нагрівання речовини. Виключивши температуру за допомогою рівняння стану та підставивши наведений вище вираз для зміни ентальпій у рівняння Гюгоніо, отримуємо рівняння Гюгоніо, виражене лише через тиск і густину,
де — показник адіабати, який для повітря кімнатної температури (298 Кельвінів) дорівнює 1,40. Криву Гюгоніо без тепловиділення ( ) часто називають ударним фронтом Гюгоніо. Разом із рівнянням для лінії Релея вищевказане рівняння повністю визначає стан системи. Ці два рівняння можна записати компактно, ввівши наступні безрозмірні масштаби,
Тоді рівняння лінії Релея та рівняння Гюгоніо спрощуються до
Враховуючи вищезазначені умови, перетин цих двох рівнянь на площині — визначає умови за течією. На площині — висхідна умова відповідає точці . Якщо не відбувається виділення тепла, наприклад, ударні хвилі без хімічної реакції, то . Асимптоти до ліній і на рисунку зображені пунктирними лініями. Як зазначено на рисунку, дозволена лише біла область, обмежена цими двома асимптотами, так що є додатним. Ударні хвилі та детонації відповідають верхній лівій білій області і , тобто тиск зростає, а питомий об'єм зменшується на ударному фронті (умова Чепмена — Жуге[en] для детонації полягає в тому, що лінія Релея є дотичною до кривої Гюгоніо). Дефлаграції, з іншого боку, відповідають нижній правій білій області, де і , тобто тиск зменшується, а питомий об'єм зростає на ударному фронті. Зниження тиску у полум'ї зазвичай дуже незначне, і його рідко враховують при дослідженні дефлаграції.
Для ударних хвиль і детонацій збільшення тиску на хвилі може приймати будь-які значення ; чим крутіший нахил лінії Релея, тим сильніша ударна хвиля. Навпаки, питоме об'ємне відношення обмежене кінцевим інтервалом (верхня межа виведена для випадку оскільки тиск не може приймати від'ємних значень). Якщо (двоатомний газ без збудження коливальної моди), це обмеження перетворюється на , іншими словами, ударна хвиля може збільшити густину щонайбільше в 6 разів. Для одноатомного газу, , і дозволений інтервал становить . Для двоатомних газів із збудженою коливальною модою маємо , і в результаті . Насправді відношення питомої теплоти в ударній хвилі не є постійним через молекулярну дисоціацію та іонізацію, але навіть у цих випадках відношення густин загалом не перевищує приблизно 11–13[6].
Виведення з рівнянь Ейлера
ред.Розгляньмо газ в одновимірному контейнері (наприклад, довгій тонкій трубці). Припустімо, що речовина є нев'язкою (тобто вона не виявляє ефектів в'язкості, як, наприклад, тертя об стінки трубки). Крім того, припустімо, що немає теплопередачі шляхом теплопровідності або випромінювання, і що гравітаційним прискоренням можна знехтувати. Така система може бути описана наступною системою законів збереження, відомою як одновимірні рівняння Ейлера:
-
()
-
()
-
()
де
- густина речовини,
- швидкість речовини,
- питома внутрішня енергія речовини,
- тиск речовини, і
- повна густина енергії речовини, [Дж/м3], а e — її питома внутрішня енергія
Далі припустимо, що енергія газу описується політропним калориметричним рівнянням
-
()
де — стале відношення питомих теплоємностей . Ця величина також є показником політропи для політропного процесу, який описується рівнянням
-
()
Повніший список рівнянь для різних типів речовин можна побачити у звіті NACA 1135 (1953)[7].
Умова стрибка
ред.Розгляньмо одновимірний випадок, у якому є стрибок скалярної фізичної величини , яка підпорядкована інтегральному закону збереження
-
()
для будь-яких , , . Для гладких розв'язків цю умову можна переписати як диференціальне рівняння в частинних похідних[8]
-
()
Нехай у речовині відбувається стрибок при , де і , тоді
-
=>
()
-
=>
()
Індекси 1 і 2 вказують на умови безпосередньо вище та нижче за течією від стрибка відповідно, тобто і .
Звернімо увагу, що для виведення рівняння (8) ми використали той факт, що і .
Тепер нехай і , коли і , і в граничному випадку
-
()
де ми визначили характеристику або швидкість ударного фронту . Простим діленням отримуємо
-
()
Рівняння (9) описує умову стрибка для закону збереження (6). У системі виникає ударний фронт, коли її характеристики перетинаються, і за цих умов вимога до єдиного однозначного розв'язку полягає в тому, щоб розв'язок задовольняв умові ентропії. Для фізично реальних застосувань це означає, що розв'язок має задовольняти ентропійній умові Лакса
-
()
де і дають характерні швидкості в вище та нижче за течією відповідно.
Умови ударного фронту
ред.У випадку гіперболічного закону збереження (6) ми побачили, що швидкість ударного фронту можна отримати простим діленням. Однак для одновимірних рівнянь Ейлера (1), (2) і (3) ми маємо векторну змінну стану і умови стрибка набувають вигляду
-
()
-
()
-
()
Рівняння (12), (13) і (14) відомі як умови Ренкіна — Гюгоніо для рівнянь Ейлера. Вони є наслідком застосування законів збереження в інтегральній формі для контрольного об'єму, який включає ударний фронт. Для цієї ситуації не можна отримати простим діленням. Однак, перейшовши в рухому систему координат ( , , ) і виконавши деякі алгебраїчні маніпуляції (зокрема, усунувши з перетвореного рівняння (13) з використанням перетвореного рівняння (12)), можна показати, що швидкість ударного фронту визначається як
-
()
де — швидкість звуку в речовині вище за течією[9][10][11][12][13][14].
Ударна лінія Гюгоніо і Релея в твердих тілах
ред.Для ударних хвиль у твердих тілах не вдається з перших принципів отримати вираз у замкнутій формі, такий як рівняння (15). Натомість експериментальні спостереження[15] показують, що замість цього можна використовувати лінійне співвідношення[16] (зване ударним фронтом Гюгоніо в площині us — upp), яке має вигляд
-
()
де c0 — швидкість звуку в матеріалі (при одновісному стисненні), s — параметр (нахил ударного фронту Гюгоніо), отриманий підгонкою експериментальних даних, а up = u2 — швидкість частинок усередині стиснутої області за ударним фронтом. Наведене вище співвідношення в поєднанні з рівняннями Гюгоніо для збереження маси та імпульсу можна використовувати для визначення ударного фронту Гюгоніо в площині p — v, де v — питомий об'єм (на одиницю маси)[17]:
-
()
Замість наведеного вище рівняння також можуть бути використані альтернативні рівняння стану, такі як рівняння стану Мі — Грюнайзена[en].
Ударний фронт Гюгоніо описує геометричне місце всіх можливих термодинамічних станів, у яких може існувати речовина за ударним фронтом, спроєктованим на двовимірну площину стану. Таким чином, це набір рівноважних станів і він не представляє конкретний шлях, яким матеріал зазнає перетворення.
Слабкі ударні фронти є ізентропійними, і ізентропія представляє шлях, яким матеріал навантажується від початкового до кінцевого станів хвилею стиснення зі збіжними характеристиками. У разі слабких ударних хвиль ударний фронт Гюгоніо перетворюється на ізентропу й може використовуватися безпосередньо як еквівалентний шлях. У випадку сильної ударної хвилі вже не можна робити це спрощення. Однак для інженерних розрахунків вважається, що ізентропа достатньо близька до ударного фронту Гюгоніо, щоб можна було зробити те саме припущення.
Якщо ударний фронт Гюгоніо є приблизною траєкторією навантаження між станами для еквівалентної хвилі стиснення, тоді умови стрибка для траєкторії ударного навантаження можна визначити, провівши пряму лінію між початковим і кінцевим станами. Ця лінія називається лінією Релея й описується таким рівнянням:
-
()
Межа пружності Гюгоніо
ред.Більшість твердих матеріалів зазнають пластичних деформацій при сильних ударних хвилях. Точка на ударному фронті Гюгоніо, у якій матеріал переходить із чисто пружного стану в пружно-пластичний стан, називається межею пружності Гюгоніо (Hugoniot elastic limit, HEL), а тиск, при якому відбувається цей перехід, позначається pHEL. Значення pHEL можуть коливатися від 0,2 ГПа до 20 ГПа. Вище межи пружності Гюгоніо матеріал втрачає значну частину своєї міцності на зсув і починає поводитися як рідина.
Магнітогідродинаміка
ред.Умови Ренкіна — Гюгоніо в магнітогідродинаміці цікаві для розгляду, оскільки вони дуже важливі для астрофізичних застосувань. Поперек розриву нормальна складова магнітного поля та тангенціальна складова електричного поля (у граничному випадку нескінченної провідності) мають бути безперервними. Таким чином, ми маємо[18]
де позначає різницю між значеннями будь-якої фізичної величини по обидва боки від розриву. Решта умов виглядають так[18]:
Ці умови є загальними в тому сенсі, що вони включають контактні розриви ( ), тангенціальні розриви ( ), обертальні або альфвенівські розриви ( ) та ударні хвилі ( ).
Примітки
ред.- ↑ Rankine, W. J. M. (1870). On the thermodynamic theory of waves of finite longitudinal disturbances. Philosophical Transactions of the Royal Society of London. 160: 277—288. doi:10.1098/rstl.1870.0015.
- ↑ Hugoniot, H. (1887). Mémoire sur la propagation des mouvements dans les corps et spécialement dans les gaz parfaits (première partie) [Memoir on the propagation of movements in bodies, especially perfect gases (first part)]. Journal de l'École Polytechnique (фр.). 57: 3—97. See also: Hugoniot, H. (1889) «Mémoire sur la propagation des mouvements dans les corps et spécialement dans les gaz parfaits (deuxième partie)» [Memoir on the propagation of movements in bodies, especially perfect gases (second part)], Journal de l'École Polytechnique, vol. 58, pages 1–125.
- ↑ Salas, M. D. (2006). The Curious Events Leading to the Theory of Shock Waves, Invited lecture, 17th Shock Interaction Symposium, Rome, 4–8 September (PDF).
- ↑ а б Williams, F. A. (2018). Combustion theory. CRC Press.
- ↑ Mikhelson, V.A. (1893). The normal velocity of ignition of combustible gaseous mixtures. Transactions of Moscow University. 10: 1—92.
- ↑ Zel'Dovich, Y. B., & Raizer, Y. P. (2012). Physics of shock waves and high-temperature hydrodynamic phenomena. Courier Corporation.
- ↑ Ames Research Staff (1953), Equations, Tables and Charts for Compressible Flow (PDF), Report 1135 of the National Advisory Committee for Aeronautics
- ↑ Note that the integral conservation law (6) could not, in general, be obtained from differential equation (6') by integration over because (6') holds for smooth solutions only.
- ↑ Liepmann, H. W., & Roshko, A. (1957). Elements of gasdynamics. Courier Corporation.
- ↑ Landau, L. D. (1959). EM Lifshitz, Fluid Mechanics. Course of Theoretical Physics, 6.
- ↑ Shapiro, A. H. (1953). The dynamics and thermodynamics of compressible fluid flow. John Wiley & Sons.
- ↑ Anderson, J. D. (1990). Modern compressible flow: with historical perspective (Vol. 12). New York: McGraw-Hill.
- ↑ Whitham, G. B. (1999). Linear and Nonlinear Waves. Wiley. ISBN 978-0-471-94090-6.
- ↑ Courant, R., & Friedrichs, K. O. (1999). Supersonic flow and shock waves (Vol. 21). Springer Science & Business Media.
- ↑ Ahrens, T.J. (1993), Equation of state (PDF), High Pressure Shock Compression of Solids, Eds. J. R. Asay and M. Shahinpoor, Springer-Verlag, New York: 75—113, doi:10.1007/978-1-4612-0911-9_4, ISBN 978-1-4612-6943-4
- ↑ Though a linear relation is widely assumed to hold, experimental data suggest that almost 80 % of tested materials do not satisfy this widely accepted linear behavior. See Kerley, G. I, 2006, «The Linear US-uP Relation in Shock-Wave Physics», arXiv:1306.6916; for details.
- ↑ Poirier, J-P. (2008) «Introduction to the Physics of the Earth's Interior», Cambridge University Press.
- ↑ а б Landau, Lev Davidovich, E. M. Lifshitz, Electrodynamics of continuous media. Vol. 8. elsevier, 2013. Section 70, Page 240.


