Хвильове рівняння

Хвильове́ рівня́ння — рівняння, яке описує розповсюдження хвиль у просторі.

Хвильове рівняння
Першовідкривач або винахідник	Жан Лерон д'Аламбер
Формула	$\Box _{c}u=0$
Позначення у формулі	$\square$
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Хвильове рівняння у Вікісховищі

Хвильове рівняння є зазвичай рівнянням другого порядку у часткових похідних гіперболічного типу, хоча існують хвильові рівняння інших порядків та інших типів.

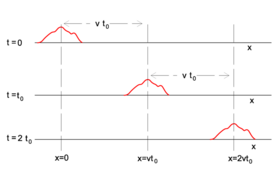
У одновимірному випадку хвильове рівняння записується так:

${\frac {\partial ^{2}u}{\partial x^{2}}}-{\frac {1}{s^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}=0,$

де u — невідома функція, яка описує хвилю, x — просторова координата, t — час, s — фазова швидкість поширення хвилі.

Розв'язки

Хвильові рівняння мають багато можливих розв'язків. Реалізація того чи іншого із них залежить від граничних та початкових умов: від того, як хвиля народилася, які перешкоди зустрічає на своєму шляху тощо.

Загальний розв'язок хвильового рівняння подається суперпозицією функцій типу

$u=u_{0}\cos(kx-\omega t-\varphi ),$

де $u_{0}$ — амплітуда хвилі, k — хвильове число, ω — циклічна частота, $\varphi$ — фаза хвилі.

Хвильове число та частота зв'язані між собою дисперсійним співвідношенням

$k={\frac {\omega }{s}}$

Інші типи хвильових рівнянь

Вільна частка описується у квантовій механіці рівнянням Шредінгера. Це рівняння параболічного типу, проте комплексне.

Дисперсійне співвідношення у ньому зв'язує енергію частки із її хвильовим вектором.

У релятивістській квантовій механіці використовуються рівняння Дірака, рівняння Клейна-Гордона тощо. Ці рівняння теж описують поширення хвиль, тож належать до групи хвильових рівнянь.

Інтернет-ресурси

• Nonlinear Wave Equations by Stephen Wolfram and Rob Knapp, Nonlinear Wave Equation Explorer by Wolfram Demonstrations Project.
• Mathematical aspects of wave equations are discussed on the Dispersive PDE Wiki
• Graham W Griffiths and William E. Schiesser (2009). Linear and nonlinear waves. Scholarpedia, 4(7):4308. doi:10.4249/scholarpedia.4308