Серединний трикутник

Серединний трикутник ^:стор.18 (додатковий трикутник) — трикутник $\triangle M_{A}M_{B}M_{C}$, вершинами якого є середини сторін даного базового трикутника $\triangle ABC$.

Червоний трикутник — серединний трикутник для чорного трикутника. Вершини червоного трикутника є серединами сторін чорного трикутника.

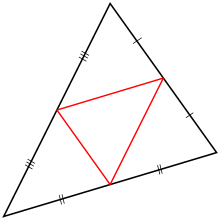
Сторони серединного трикутника є середніми лініями $\triangle ABC$.

Є окремим випадком серединного багатокутника при кількости сторін багатокутника $n=3$.

Властивості

M: центр описаного кола △ABC, ортоцентр △DEF
N: центр вписаного кола △ABC, точка Нагеля △DEF
S: центроїд △ABC та △DEF

• Серединний трикутник $\triangle M_{A}M_{B}M_{C}$ є образом даного початкового трикутника $\triangle ABC$ при гомотетії з центром у центроїді та коефіцієнтом $k=-{\frac {1}{2}}$.
  Таким чином, серединний трикутник подібний до початкового і має той самий центроїд і ті самі медіани, що й початковий трикутник $\triangle ABC$. Довжини сторін серединногоо трикутника вдвічі менші за довжини сторін початкового трикутника $\triangle ABC$.
• Периметр серединного трикутника $\triangle M_{A}M_{B}M_{C}$ дорівнює півпериметру трикутника $\triangle ABC$, а його площа дорівнює чверті площі трикутника $\triangle ABC$. ^{:стор.177}
• Чотири трикутники, на які розділяється початковий трикутник $\triangle ABC$ сторонами його серединного трикутника $\triangle M_{A}M_{B}M_{C}$, рівні за трьома сторонами, тому їхні площі рівні.
  Через це іноді «серединними» називають одразу всі чотири, рівні між собою, внутрішні трикутники, одержані з початкового трикутника проведенням у ньому трьох середніх ліній (у термінології серединним називають тільки один з них — центральний).
• Ортоцентр серединного трикутника $\triangle M_{A}M_{B}M_{C}$ збігається з центром описаного кола даного трикутника $\triangle ABC$, що доводить належність центра описаного кола, центроїда й ортоцентра одній прямій — прямій Ейлера.
• Серединний трикутник є подерним трикутником центра описаного кола трикутника відносно трикутника $\triangle ABC$.
• Коло дев'яти точок трикутника $\triangle ABC$ є описаним для його серединного трикутника $\triangle M_{A}M_{B}M_{C}$, а тому центр кола дев'яти точок $\triangle ABC$ є центром кола, описаного навколо серединного трикутника

$\triangle M_{A}M_{B}M_{C}$.

• Точка Нагеля серединного трикутника є центром вписаного кола початкового трикутника $\triangle ABC$. ^{:стоp.161,Теор.337}
• Серединний трикутник конгруентний до трикутника, вершинами якого є середини відрізків, що з'єднують ортоцентр і вершини початкового трикутника $\triangle ABC$.^{:стор.103,#206;стор.108,#1}
• Центр вписаного кола трикутника $\triangle ABC$ лежить всередині його серединного трикутника $\triangle M_{A}M_{B}M_{C}$.^{:стор.233, лемма 1}

Точка всередині трикутника є центром вписаного у трикутник еліпса тоді й тільки тоді, коли ця точка лежить усередині серединного трикутника. ^:стоp.139

• Серединний трикутник є єдиним вписаним трикутником, для якого жоден із трьох інших трикутників не має площу, меншу за площу цього трикутника. ^{:стоp. 137}
• Центр кола, вписаного в серединний трикутник даного трикутника $\triangle ABC$, є центром мас периметра трикутника $\triangle ABC$ (центром Шпікера); ^:стор.19
  Тобто цей центр є центром мас однорідної дротяної фігури, що відповідає трикутнику $\triangle ABC$.

Координати

Нехай $a=\left|BC\right|$, $b=\left|CA\right|$, $c=\left|AB\right|$ - довжини сторін трикутника $\triangle ABC$. Тоді трилінійні координати вершин серединного трикутника задаються формулами:

${\begin{cases}X=\left(0;{\frac {1}{b}};{\frac {1}{c}}\right)\\Y=\left({\frac {1}{a}};0;{\frac {1}{c}}\right)\\Z=\left({\frac {1}{a}};{\frac {1}{b}};0\right)\end{cases}}$

Антисерединний трикутник

Якщо $\triangle XYZ$ — серединний трикутник для $\triangle ABC$, то $\triangle ABC$ є антисерединним трикутником для $\triangle XYZ$. Антисерединний трикутник для $\triangle ABC$ утворюється трьома прямими, паралельними сторонам $\triangle ABC$ — паралельно AB через точку C, паралельно AC через точку B і паралельно BC через точку A.

Трикутні координати вершин антисерединного трикутника $\triangle X'Y'Z'$ задаються формулами:

${\begin{cases}X'=\left(-{\frac {1}{a}};{\frac {1}{b}};{\frac {1}{c}}\right)\\Y'=\left({\frac {1}{a}};-{\frac {1}{b}};{\frac {1}{c}}\right)\\Z'=\left({\frac {1}{a}};{\frac {1}{b}};-{\frac {1}{c}}\right)\end{cases}}$

Література

• Alfred S. Posamentier, Ingmar Lehmann. {{{Заголовок}}}. — Prometheus Books, 2012 (мова: англ.).

• Зетель С.И. Новая геометрия треугольника. Пособие для учителей. — изд.2. — москва : Учпедгиз, 1962 (мова: рашистська).

• Coxeter H. S. M.; Greitzer S. L. §1.7 "The Medial Triangle and Euler Line." // Geometry Revisited. — Washington : Math. Assoc. Amer, 1967 (мова: англ.). — Vol. 19.

Посилання

• Weisstein, Eric W. Medial triangle(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Anticomplementary Triangle(англ.) на сайті Wolfram MathWorld.