Зрізаний кубооктаедр
Зрізаний кубооктаедр — напівправильний многогранник (архімедове тіло) з 12 квадратними гранями, 8 гранями у вигляді правильного шестикутника, 6 гранями у вигляді правильного восьмикутника, 48 вершинами і 72 ребрами. Оскільки кожна з граней многогранника має центральну симетрію (що еквівалентно повороту на 180°), зрізаний кубооктаедр є зоноедром.
| Зрізаний кубооктаедр | |
|---|---|
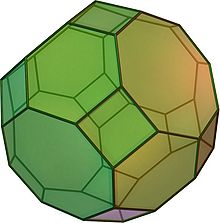 | |
| Тип | напівправильний многогранник |
| Граней | 26: 12 квадратних, 8 шестикутних, 6 восьмикутник |
| Ребер | 72 |
| Вершин | 48 |
| Конфігурація вершин | 4.6.8 |
| Символ Витофа | 2 3 4 | |
| Символ Шлефлі | tr{4,3} або |
| Діаграма Коксетера | |
| Група симетрії | Oh, B3, [4,3], (*432), порядок 48 |
| Площа поверхні | |
| Об'єм | |
| Двогранний кут (градуси) | 4-6: arccos(−√6/3) = 144°44′08″ 4-8: arccos(−1/√2) = 135° 6-8: arccos(−√3/3) = 125°15′51″ |
| Дуальний многогранник | гекзакісоктаедр |
| напівправильний опуклий многогранник, зоноедр | |
| Вершинна діаграма | |
 | |
| Розгортка | |
 | |
Інші назви
ред.Цей многогранник має кілька назв:
- Зрізаний кубооктаедр (Йоганн Кеплер)
- Ромбозрізаний кубооктаедр (Маґнус Веннінґер[1][2])
- Великий ромбокубооктаедр (Роберт Вільямс[en][3])
- Великий ромбокубооктаедр (Пітер Кромвель[4])
- Загальнозрізаний куб (omnitruncated cube) або скіс-зрізаний куб (cantitruncated cube) (Норман Джонсон[en])
Назва зрізаний кубооктаедр, яку дав спочатку Йоганн Кеплер, дещо вводить в оману. Зрізання кубооктаедра відсіканням кутів (вершин) не дозволяє отримати цю однорідну фігуру, оскільки деякі грані будуть прямокутниками. Однак отримана фігура топологічно еквівалентна зрізаному кубооктаедру та її завжди можна деформувати до стану, коли грані стануть правильними.
Альтернативна назва — великий ромбокубооктаедр — посилається на той факт, що 12 квадратних граней лежать у тих самих площинах, що й 12 граней ромбододекаедра, який двоїстий кубооктаедру. (Порівн. малий ромбокубооктаедр)
Також існує неопуклий однорідний многогранник з такою ж назвою — неопуклий великий ромбокубооктаедр[en].
Декартові координати
ред.Декартові координати вершин зрізаного кубооктаедра, що має ребро довжини 2 і центр у початку координат, є перестановками чисел:
- (±1, ±(1+√2), ±(1+2√2))
Площа та об'єм
ред.Площа та об'єм зрізаного кубооктаедра з ребром довжини a рівні:
Розрізання
ред.Зрізаний кубооктаедр можна розрізати на частини, отримавши центральний ромбокубооктаедр з 6 квадратними куполами над первинними квадратними гранями, 8 трикутними куполами над трикутними гранями і 12 кубами над вторинними квадратними гранями.
Зі зрізаного кубооктаедра можна отримати тороїди Стюарта роду 5, 7 або 11, якщо видалити центральний ромбокубооктаедр або квадратні куполи, або трикутні куполи, або 12 кубів відповідно. Можна побудувати багато інших тороїдів із меншим ступенем симетрії, видаляючи підмножини цих компонентів. Наприклад, видалення половини трикутних куполів дає тороїд роду 3, який (за правильного вибору куполів, що видаляються) має тетраедричну симетрію[5][6].
| Рід 3 | Рід 5 | Рід 7 | Рід 11 |
|---|---|---|---|
Однорідні розфарбування
ред.Існує лише одне однорідне розфарбування граней цього многогранника, по одному кольору на кожен тип грані.
Існує 2-однорідне розфарбування з тетраедричною симетрією з розфарбуванням шестикутників у два кольори.
Ортогональні проєкції
ред.Зрізаний кубооктаедр має дві особливі ортогональні проєкції на площини Коксетера A2 і B2 з [6] і [8] проєктивними симетріями, і багато [2] симетрій можна побудувати, виходячи з різних площин проєкції.
Сферичні мозаїки
ред.Зрізаний кубооктаедр можна подати як сферичну мозаїку і спроєктувати на площину за допомогою стереографічної проєкції. Ця проєкція конформна, вона зберігає кути, але не зберігає довжин та площ. Прямі лінії на сфері проєктуються в колові дуги на площині.
| квадрат- центрована |
шестикутник- центрована |
восьмикутник- центрована | |
| Ортогональна проекція | Стереографічні проекції | ||
|---|---|---|---|
Пов'язані многогранники
ред.Зрізаний кубооктаедр входить у сімейство однорідних многогранників, пов'язаних із кубом і правильним октаедром.
| Однорідні октаедричні многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симетрія: [4,3], (*432)[en] | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
| = |
= |
= |
= or |
= or |
= | |||||
| |
|
|
|
| ||||||
| Двоїсті многогранники | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
| Файл:RhombicDodecahedron.svg | Файл:DisdyakisDodecahedron.svg | |||||||||
Цей многогранник можна вважати членом послідовності однорідних вершинних фігур зі схемою (4.6.2p) та діаграмою Коксетера — Динкіна . Для p < 6 члени послідовності є всезрізаними[en] многогранниками (зоноедрами), показаними нижче як сферичні мозаїки. Для p > 6 вони є мозаїками на гіперболічній площині, починаючи зі зрізаної трисемикутної мозаїки[en].
| Симетрія *n32[en] n,3[en] |
Сферична | Евклідова[en] | Компактна гіперболічна | Паракомп. | Некомпактна гіперболічна | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Фігури | ||||||||||||
| Конфігурація | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12[en] | 4.6.14[en] | 4.6.16[en] | 4.6.∞[en] | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Двоїста | ||||||||||||
| Конфігурація грані | V4.6.4[en] | V4.6.6 | V4.6.8[en] | V4.6.10 | V4.6.12[en] | V4.6.14[en] | V4.6.16[en] | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Граф зрізаного кубооктаедра
ред.| Граф зрізаного кубооктаедра | |
|---|---|
| Вершин | 48 |
| Ребер | 72 |
| Автоморфізм | 48 |
| Хроматичне число | 2 |
| Властивості | кубічний
нуль-симетричний[en] |
У теорії графів граф зрізаного кубооктаедра (або граф великого ромбокубооктаедра) — граф вершин і ребер зрізаного кубооктаедра. Він має 48 вершин і 72 ребра, нуль-симетричний[en] і є кубічним архімедовим графом[7].
Примітки
ред.- ↑ Веннинджер, 1974, с. 20, 39.
- ↑ Wenninger, 1974, с. 29.
- ↑ Williams, 1979, с. 82.
- ↑ Cromwell, 1997, с. 82.
- ↑ Stewart, 1970.
- ↑ Adventures Among the Toroids — Chapter 5 — Simplest (R)(A)(Q)(T) Toroids of genus p=1. Архів оригіналу за 4 лютого 2016. Процитовано 8 листопада 2015.
{{cite web}}: символ нерозривного пробілу в|title=на позиції 29 (довідка) - ↑ Read, Wilson, 1998, с. 269.
Література
ред.- М. Веннинджер. Модели многогранников. — Мир, 1974.
- Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича[ru], А. Я. Хинчина[ru]. — М. : Государственное издательство физико-математической литературы[ru], 1963. — С. 382—447.
- Л. А. Люстерник. Выпуклые фигуры и многогранники. — М. : Государственное издательство технико-теоретической литературы[ru], 1956.
- Magnus Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — ISBN 978-0-521-09859-5. (Модель 15, стор. 29)
- Robert Williams. The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc, 1979. — ISBN 0-486-23729-X. (Секція 3-9, стор. 82)
- P. Cromwell. Polyhedra. — United Kingdom : Cambridge, 1997. — С. 79–86 Archimedean solids. — ISBN 0-521-55432-2.
- R.C. Read, R.J. Wilson. An Atlas of Graphs. — Oxford University Press, 1998.
- B. M. Stewart. Adventures Among the Toroids. — 1970. — ISBN 978-0-686-11936-4.
Посилання
ред.- Weisstein, Eric W. Great rhombicuboctahedral graph(англ.) на сайті Wolfram MathWorld.
- 3D convex uniform polyhedra
- Editable printable net of a truncated cuboctahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- great Rhombicuboctahedron: paper strips for plaiting


