Коловий рух
Колови́й рух або рух по ко́лу (англ. circular motion) — механічний рух у вигляді обертання навколо фіксованої осі матеріальної точки або тіла, коли вісь обертання в обраній системі відліку не проходить через цю матеріальну точку чи центр тіла. У цьому випадку траєкторія руху точки або усіх точок тіла є колом, коловою орбітою. Рух може бути рівномірним (зі сталою кутовою швидкістю) або нерівномірним (із змінною кутовою швидкістю). Обертання тривимірного тіла навколо фіксованої осі включає коловий рух кожної його частки. У загальнішому випадку про рух по колу об'єкта можна говорити якщо знехтувати його розмірами, а розглядати лише рух по колу його центра мас.
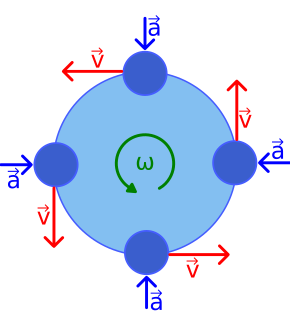
Приклади колового руху: штучний супутник на геосинхронній орбіті, тягарець на шнурку при обертанні по колу (наприклад, метання молота), болід, що рухається трасою на повороті, виконаному по коловій дузі, електрон, що рухається перпендикулярно до постійного магнітного поля тощо.
Рух по колу є прискореним, навіть якщо відбувається з постійною кутовою швидкістю, бо вектор швидкості об'єкта постійно змінює напрямок. Така зміна напрямку швидкості потребує доцентрового прискорення рухомого об'єкта доцентровою силою, яка штовхає його у напрямку до центра колової орбіти. Без цього прискорення об'єкт рухатиметься прямолінійно відповідно до законів Ньютона.
Формули для рівномірного колового руху
ред.Для руху по колу радіуса R довжина кола буде C = 2π R. Якщо період обертання є T, то кутова швидкість обертання ω буде дорівнювати:
Швидкість руху об'єкта дорівнює
Кут повороту θ за час t становить:
Прискорення, що спричиняє зміну напряму швидкості, можна визначити, якщо врахувати, що швидкість робить повну зміну напряму за цей же час T, за який об'єкт робить один повний оберт. Тоді вектор швидкості проходить шлях довжиною 2π v кожні T секунд, або:
і спрямоване радіально до центра.
Взаємозв'язки векторів показано на рисунку. Вісь обертання зображена вектором Ω, перпендикулярним до площини орбіти і має величину ω = dθ / dt. Напрям вектора Ω обрано відповідно до правилом правої руки. За цим правилом швидкість це векторний добуток виду:
і є вектором, перпендикулярним як до Ω так і до r (t), спрямованим по дотичній до орбіти та величиною ω R. Аналогічно, прискорення визначається як:
Воно являє собою вектор, перпендикулярний як до Ω так і до v (t), та величиною ω |v| = ω2 R й спрямований строго протилежно до r (t).
Постійна швидкість
ред.У найпростішому випадку швидкість, маса і радіус є сталими.
Розглянемо тіло масою один кілограм, що рухається по колу радіусом один метр з кутовою швидкістю один радіан за секунду.
- Швидкість: один метр за секунду;
- Радіальне прискорення: один метр на секунду за секунду;
- Прискорення створюється доцентровою силою один кілограм на метр на секунду за секунду, тобто один ньютон;
- Імпульс тіла: один кілограм на метр за секунду (кг٠м٠с-1);
- Момент інерції: один кілограм на метр в квадраті (кг٠м2);
- Момент імпульсу: один кілограм на метр в квадраті за секунду (кг٠м2٠с-1);
- Кінетична енергія: джоуля;
- Окружність орбіти: метрів;
- Період руху: секунд на оберт;
- Частота: герц;
- З точки зору квантової механіки система перебуває у збудженому стані з квантовим числом
Тепер розглянемр тіло маси , що рухається по колу радіусом з кутовою швидкістю
- Швидкість:
- Радіальне прискорення:
- Доцентрова сила:
- Імпульс тіла:
- Момент інерції:
- Момент імпульсу:
- Кінетична енергія:
- Довжина кола орбіти:
- Період руху:
- Частота: . (Замість літери частота часто позначається грецькою літерою , яку, однак, часто можна сплутати з літерою , що використовується для позначення швидкості);
- Квантове число: где — Стала Планка
Змінна швидкість
ред.У коловому русі повну силу, прикладену до об'єкта, можна розкласти на дві складові: доцентрову, що утримує тіло на коловій орбіті (тобто змінює напрямок вектора швидкості), і тангенціальну, спрямовану по дотичній до кола й викликає зміну довжини вектора швидкості (що змінює швидкість обертання тіла по орбіті). Величина доцентрової складової залежить від миттєвої швидкості.
Наприклад, коли камінь прив'язаний до кінця мотузки, він зазнає впливу деякої сили, яку ми можемо розкласти на радіальну і бічну (дотичну) складові. Радіальна спрямована до центра (всередину) кола і викликана тим, що мотузка чинить опір своєму видовженню. А бічна складова визначає як обертання каменя прискорюватиметься чи сповільнюватиметься.
Опис колового руху у полярних координатах
ред.Траєкторія колового руху тіла може бути описана в полярній системі координат значеннями фіксованої відстані R від центра орбіти, що є точкою відліку, і кута орієнтації θ (t) від деякого фіксованого напряму (див. рис.). Вектор переміщення є радіальним вектором від полюса до поточного положення:
де — одиничний вектор, паралельний до радіуса в момент t і спрямований від полюса. Зручно також увести одиничний вектор, ортогональний до , який позначимо . Зазвичай його орієнтація обирається за напрямом руху уздовж орбіти.
Швидкість є похідною від переміщення по часу:
Оскільки радіус кола є константою, радіальна складова швидкості дорівнює нулю. Одиничний вектор має інваріантне по часу значення, так що при зміні часу його кінець завжди лежить на колі одиничного радіуса, а кут θ такий же, як у . Якщо відбувся малий приріст кута dθ за час dt, тоді описує дугу одиничного кола зі значенням dθ (див. одиничне коло на рисунку ліворуч). Отже:
де напрям зміни має бути перпендикулярним до (або, іншими словами, уздовж ), бо будь-яка зміна d у напрямі буде змінювати величину . Знак додатній, тому що зростання dθ впливає на об'єкт і пересувається у напрямі .
Отже, швидкість стає рівною:
Прискорення тіла також можна розкласти на радіальну та тангенціальну складові. Прискорення є похідною швидкості по часу:
Похідна по часу від знаходиться таким же шляхом, як і для . Знову ж, — одиничний вектор, і його кінець розташований на одиничному колі, а кут дорівнює π/2 + θ. Отже, приріст кута dθ вектора переміщує по дузі на величину dθ, і оскільки є перпендикулярний до , маємо:
де від'ємний знак потрібен, щоб зберегти перпендикулярним до . (В іншому випадку кут між і буде зменшуватись зі збільшенням dθ, див. одиничне коло ліворуч на рисунку). Отже, прискорення дорівнює:
Доцентрове прискорення — це радіальна складова, спрямована по радіусу до середини:
тоді як тангенціальна складова змінює значення швидкості:
Опис колового руху в комплексних числах
ред.Коловий рух можна описати з використанням комплексних чисел. Нехай — вісь дійсних чисел, а — вісь уявних чисел. Тоді положення тіла може бути заданим у вигляді комплексного «вектора» :
де уявна одиниця, і
є кутом комплексного вектора відносно дійсної осі як функція часу t.
Оскільки радіус є константою:
де крапка означає диференціал по часу. У цих позначеннях швидкість має вигляд :
а прискорення:
Перший доданок спрямований проти вектора переміщення, а другий перпендикулярно до нього, як і у попередніх результатах.
Див. також
ред.Посилання
ред.- Mathematics of Circular Motion [Архівовано 24 березня 2022 у Wayback Machine.] // Physics Classroom (англ.)
- Uniform Circular Motion: Crash Course Physics #7 [Архівовано 6 квітня 2022 у Wayback Machine.] // CrashCourse (англ.)