Торичний вузол
Торичний вузол — особливий вид вузлів, що лежать на поверхні незавузленого тора в .


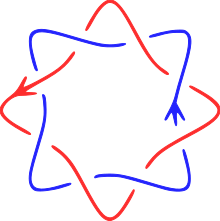
Торичне зачеплення — зачеплення, що лежить на поверхні тора.
Кожен торичний вузол визначається парою взаємно простих цілих чисел і . Торичне зачеплення виникає, коли і не взаємно прості (в цьому випадку число компонент дорівнює найбільшому спільному дільнику і ). Торичний вузол є тривіальним тоді і тільки тоді, коли або , або дорівнює 1 або -1. Найпростішим нетривіальним прикладом є (2,3)-торичний вузол, відомий також як трилисник.

Геометричне подання
ред.Торичний вузол можна подати геометрично різними способами, топологічно еквівалентними, але геометрично різними.
Зазвичай використовується домовленість, що -торичний вузол обертається разів навколо кругової осі тора і разів навколо осі обертання тора. Якщо і не взаємно прості, то виходить торичне зачеплення, що має більше однієї компоненти. Домовленості про напрямок обертання ниток навколо тора також різні, найчастіше припускається правий гвинт для [1][2][3].
-торичний вузол можна задати параметризацією:
- ,
- ,
- ,
де і . Він лежить на поверхні тора, що задається формулою (в циліндричних координатах).
Можливі й інші параметризації, оскільки вузли визначені з точністю до неперервної деформації. Приклади для (2,3)- і (3,8)-торичних вузлів можна отримати, прийнявши , а в разі (2,3)-торичного вузла — шляхом віднімання і з наведених вище параметризацій і .
Властивості
ред.Торичний вузол є тривіальним тоді і тільки тоді, коли або , або дорівнює 1 або -1 [2] [3] .
Кожен нетривіальний торичний вузол є простим і хіральним.
-торичний вузол еквівалентний -торичному вузлу[1][3]. -торичний вузол є оберненим (дзеркальним відображенням) -торичного вузла[3]. -торичний вузол еквівалентний -торичному вузлу, за винятком орієнтації.
Будь-який -торичний вузол можна побудувати з замкнутої коси з нитками. Відповідне слово коси[4]:
- .
Ця формула використовує домовленість, що генератори коси використовують праві обертання[2][4][5][6].
Число перетинів -торичного вузла з задається формулою:
- .
Рід торичного вузла з дорівнює:
Многочлен Александера торичного вузла дорівнює[1][4]:
- .
Многочлен Джонса (правогвинтовий) торичного вузла задається формулою:
- .
Доповнення торичного вузла на 3-сфері — це многовид Зейферта.
Нехай — -мірний блазенський ковпак з диском, видаленим всередині, — -вимірний блазенський ковпак з диском, видаленим всередині, і — фактор-простір, отриманий ототожненням і вздовж межі кола. Доповнення -торичного вузла є деформаційним ретрактом простору . Таким чином, група вузла торичного вузла має подання:
- .
Торичні вузли — це єдині вузли, чиї групи вузла мають нетривіальні центри (які є нескінченними циклічними групами, утвореними елементом з цього подання).
Перелік
ред.- Тривіальний вузол, 31-вузол (2,3), вузол «Перстач» (5,2), вузол 7₁ (7,2), вузол 819 (4,3), вузол 91 (9,2), вузол 10124 (5,3).
Див. також
ред.Примітки
ред.- ↑ а б в Livingston, 1993.
- ↑ а б в Murasugi, 1996.
- ↑ а б в г Kawauchi, 1996.
- ↑ а б в Lickorish, 1997.
- ↑ Dehornoy, P. et al. (2000). Why are braids orderable? http://www.math.unicaen.fr/~dehornoy/Books/Why/Dgr.pdf [Архівовано 15 квітня 2012 у Wayback Machine.]
- ↑ Birman, Brendle, 2005.
Література
ред.- Charles Livingston. Knot theory. — Mathematical Association of America, 1993. — ISBN 0-88385-027-3.(англ.)
- Kunio Murasugi. Knot theory and its applications. — Birkhäuser, 1996. — ISBN 3-7643-3817-2.(англ.)
- Akio Kawauchi. A survey of knot theory. — Birkhäuser, 1996. — ISBN 3-7643-5124-1.(англ.)
- W. B. R. Lickorish. An introduction to knot theory. — Springer, 1997. — ISBN 0-387-98254-X.(англ.)
- J. S. Birman, T. E. Brendle. Handbook of knot theory / W. Menasco, M. Thistlethwaite. — Elsevier, 2005. — ISBN 0-444-51452-X..(англ.)
- J. Milnor. Singular Points of Complex Hypersurfaces. — Princeton University Press, 1968. — ISBN 0-691-08065-8.(англ.)
Посилання
ред.- Про поліноми Чебишова і торичні вузли
- 36 Torus Knots, The Knot Atlas.
- Weisstein, Eric W. Torus Knot(англ.) на сайті Wolfram MathWorld.
- Torus knot renderer in Actionscript
- Fun with the PQ-Torus Knot


